动态DP实例讲解

一、简介

有一类问题，它可以采用 DP 解决。但是，如果我们加入区间查询，单点修改甚至区间修改，普通DP望尘莫及。于是，动态DP就应运而生了。

二、例题

例题一：给定一个长度为 n 的序列，你需要维护两种操作：

①查询一个区间的最大子段和；

②单点修改(即将一个位置上的数改成另一个数)

Solution

首先，考虑这样一道题目：求出整个序列的最大子段和，没有修改。

令表示以 i 为结尾的区间的最大和，则不难得到状态转移：

令表示 [1,i] 的最大子段和，不难得到

边界：

答案：

加入了单点修改以及区间查询之后，我们该怎么办呢？

观察一下我们的状态转移，可以发现——从转移到的转移式，仅仅与有关。这启发我们去给每个位置设定一个矩阵，并通过矩阵乘法来表示 f 的转移。

但是，转移式中含有max，不符合普通矩阵乘法的形式。不慌！我们可以大胆地重定义矩阵乘法 A ⋅ B = C：

从而，我们就写出了 f 的转移与 i 之间的关系：

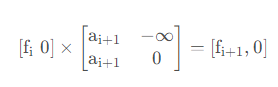
这样只能求出 f，而并不能求出我们所真正需要的 m 。所以，我们在矩阵中再加入一行一列来表示 m 的转移与f，i 的关系。

从而，我们得到了最终的式子：

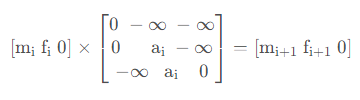
对于一次形如 [L,R] 的查询，我们初始化，然后依次将乘上 L , L+1 , ⋯   , R 处的矩阵即可。

暴力乘显然超时，考虑优化。注意到这个矩阵乘法是有结合率的，于是我们采用线段树来维护区间矩阵积，查询的时候直接用向量依次乘上 O(logn) 个矩阵即可。

对于一次单点修改，它只会导致一个矩阵的改变，于是在线段树上执行一次单点修改即可。

时间复杂度

例题二：给定一棵大小为 n 的树，每个节点有一个点权；q 次操作，每次单点修改或查询整棵树的最大独立集。

Solution

刚才我们所讨论的例 1 是序列上的问题。现在我们将它搬到了树上，显然无法凑效了。

依然先考虑不带修的情况。

令表示，在 i 子树中的最大独立子集；表示节点 i 不能选，表示 i 必须选。

状态转移:

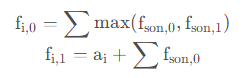
不难发现，对一个节点的点权进行改变后，只会改变它以及它祖先的一些 f 值。但是，这棵树可能会退化成一条链，从而使得每次要修改的节点的数量很多。

考虑使用树链剖分来优化这一步骤。

令 i 的重儿子是 ws，，，则不难得到

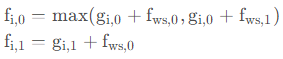
与序列上的动态 dp 类似，可以设计一个广义矩阵乘法来完成转移：

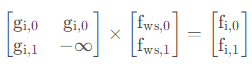
若修改了 i 的点权，我们先在 i 处做单点修改，并不停地往上跳重链，通过线段树求出当前重链的矩阵乘积；同时，也要记得在跳到的链顶的父亲处做单点修改。

时间复杂度