什么是动态规划?

谈到动态规划，很多人会疑惑动态规划难吗？说实话很难，特别是对于初学者来说，入门动态规划的时候，举个例子，看 0-1背包问题，很容易就被题目弄懵了。就算看的懂答案，但就是自己不会做，不知道怎么下手。就像做递归的题，看的懂答案，但下不了手。

对于动态规划，好多题都会用到，如果你对动态规划感兴趣，或者你不知道怎么下手，那么这篇文章的将会系统的介绍什么是动态规划，帮助大家做题。

为了兼顾初学者，我会从最简单的题讲起，后面会越来越难，最后面还会讲解，该如何优化。因为 80% 的动规都是可以进行优化的。不过我得说，如果你连动态规划是什么都没听过，可能这篇文章你也会压力山大。

一、什么是动态规划?

动态规划算法是新手在刚接触算法设计时很苦恼的问题，有时候觉得难以理解，但是真正理解之后，就会觉得动态规划其实并没有想象中那么难。

动态规划(Dynamic Programming)是一种分阶段求解决策问题的数学思想，它通过把原问题分解为简单的子问题来解决复杂问题，动态规划在很多领域都有着广泛的应用,例如管理学，经济学，数学，生物学，等等。

（1）动态规划适用于解决带有最优子结构和子问题重叠性质的问题

1. 最优子结构 : 即是局部最优解能够决定全局最优解(也可以认为是问题可以被分解为子问题来解决),如果问题的最优解所包含的子问题的解也是最优的，我们就称该问题具有最优子结构性质。

2. 子问题重叠 : 即是当使用递归进行自顶向下的求解时,每次产生的子问题不总是新的问题,而是已经被重复计算过的问题.动态规划利用了这种性质,使用一个集合将已经计算过的结果放入其中,当再次遇见重复的问题时,只需要从集合中取出对应的结果。

（2）动态规划与分治算法的区别

相信了解过分治算法的同学会发现，动态规划与分治算法很相似，下面我们例举出一些它们的相同之处与不同之处。

相同点：

1. 分治算法与动态规划都是将一个复杂问题分解为简单的子问题。

2. 分治算法与动态规划都只能解决带有最优子结构性质的问题。

不同点：

1. 分治算法一般都是使用递归自顶向下实现，动态规划使用迭代自底向上实现或带有记忆功能的递归实现。

2. 动态规划解决带有子问题重叠性质的问题效率更加高效。

3.分治算法分解的子问题是相对独立的。

4. 动态规划分解的子问题是互相带有关联且有重叠的。

（3）斐波那契数列

斐波那契数列就很适合使用动态规划来求解，它在数学上是使用递归来定义的,公式为F(n) = F(n-1) + F(n-2)

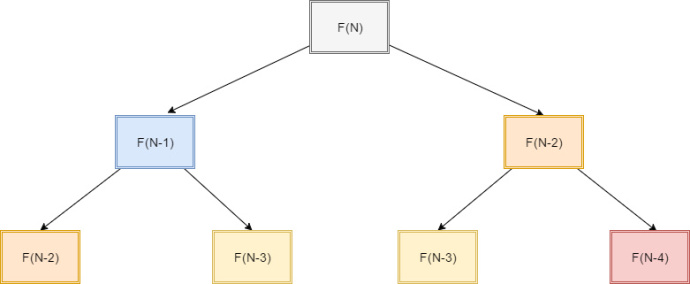
斐波那契数列求解过程

普通递归实现

一个最简单的实现如下：

    public int fibonacci(int n) {
        if (n < 1)
            return 0;
        if (n == 1)
            return 1;
        if (n == 2)
            return 2;
 
        return fibonacci(n - 1) + fibonacci(n - 2);
    }

但这种算法并不高效，它做了很多重复计算，它的时间复杂度为O(2^n)。

动态规划递归实现

使用动态规划来将重复计算的结果具有"记忆性"，就可以将时间复杂度降低为O(n)。

    public int fibonacci(int n) {
        if (n < 1)
            return 0;
        if (n == 1)
            return 1;
        if (n == 2)
            return 2;
 
        // 判断当前n的结果是否已经被计算,如果map存在n则代表该结果已经计算过了
        if (map.containsKey(n))
            return map.get(n);
 
        int value = fibonacci(n - 1) + fibonacci(n - 2);
        map.put(n, value);
        return value;
    }

虽然降低了时间复杂度，但需要维护一个集合用于存放计算结果，导致空间复杂度提升了。

动态规划迭代实现

通过观察斐波那契数列的规律，发现n只依赖于前2种状态，所以我们可以自底向上地迭代实现。

    public int fibonacci(int n) {
        if (n < 1)
            return 0;
        if (n == 1)
            return 1;
        if (n == 2)
            return 2;
 
        // 使用变量a,b来保存上次迭代和上上次迭代的结果
        int a = 1;
        int b = 2;
        int temp = 0;
 
        for (int i = 3; i <= n; i++) {
            temp = a + b;
            a = b;
            b = temp;
        }
 
        return temp;
    }

这样不仅时间复杂度得到了优化，也不需要额外的空间复杂度。