悬线法实例讲解

先说说什么是悬线？就是一条竖线，这条竖线有初始位置和高度两个性质，可以在其上端点不超过当前位置的矩形高度的情况下左右移动。

一、概述

悬线法的适用范围是单调栈的子集。具体来说，悬线法可以应用于满足以下条件的题目：

（1）需要在扫描序列时维护单调的信息；

（2）可以使用单调栈解决；

（3）不需要在单调栈上二分。

看起来悬线法可以被替代，用处不大，但是悬线法概念比单调栈简单，更适合初学 OI 的选手理解并解决最大子矩阵等问题。

二、实例讲解

悬线法是一种比较简单的DP技巧，主要用于在的时间内解决最大矩形/最大正方形问题，即，给出一个的方格矩阵，其中某些方格是不可选的，求可选的最大矩形/正方形。

其实这个问题用单调栈也是可以解决的，但悬线法是一种思路更简单的方法。我们定义“悬线”是从某一格出发，一直向上能延申的最长竖线（如下图）。

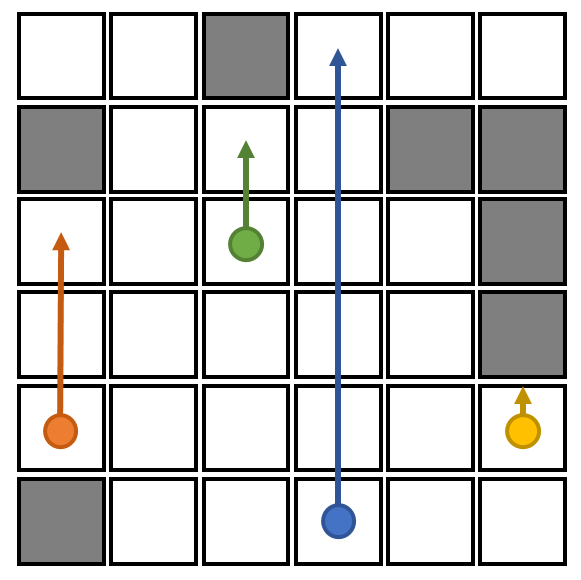
我们定义极大矩形是无法再向上、下、左或右拓展的矩形，很明显，每一个最大矩形，都一定是一个极大矩形（否则拓展后的矩形比它更大，它就不是最大的了）。

一个重要的事实是：每个极大矩形都一定可以由某条悬线“拓展”（即把悬线尽可能地往左、往右平移）得到。实际上，在矩形上边界上找到一个不能再向上的方格（作为极大矩形，一定存在这样的方格），把它跟矩形下边界的对应格连线，即可得到这样的悬线。

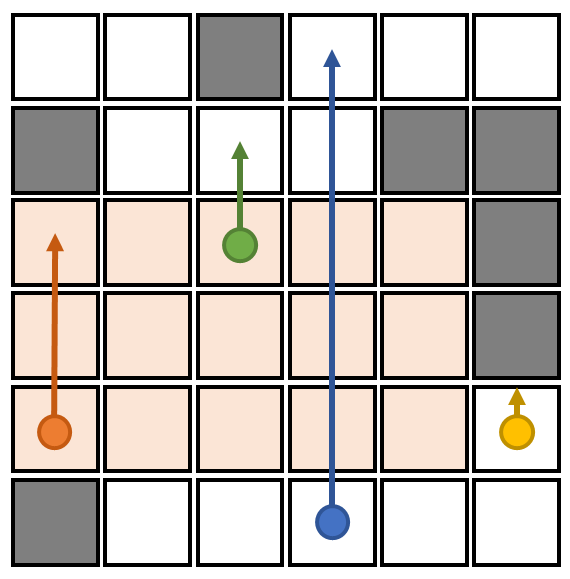
由于一个可选的格子对应一条悬线，所以悬线最多只有条。因此，我们只需要枚举最多条悬线就可以枚举所有的极大矩形，最大矩形一定就在其中。

接下来是十分简单的DP环节。定义分别表示从某格出发向上、左、右最多能走多少格（包括自身），则：

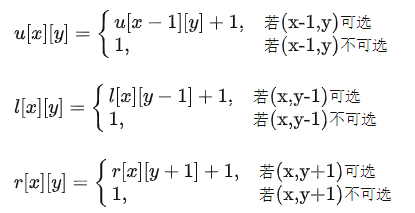
然后我们定义 L、R 分别表示从当前格向上的悬线最多能向左、向右拓展多少格，则：

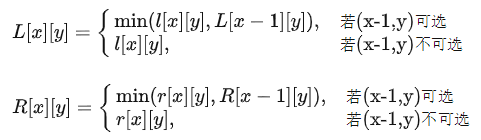
实际上我们发现分别可以用同一个数组来存，可以节省很多空间。对于每一格来说，它对应的悬线左右拓展能得到的最大的矩形面积为：

代码如下：

for (int i = 1; i <= n; ++i)
    for (int j = 1; j <= m; ++j)
        if (A[i][j])
            l[i][j] = l[i][j - 1] + 1;for (int i = 1; i <= n; ++i)
    for (int j = m; j >= 1; --j)
        if (A[i][j])
            r[i][j] = r[i][j + 1] + 1;for (int i = 1; i <= n; ++i)
    for (int j = 1; j <= m; ++j)
        if (A[i][j]) {
            u[i][j] = u[i - 1][j] + 1;
            if (A[i - 1][j]) cmin(l[i][j], l[i - 1][j]), cmin(r[i][j], r[i - 1][j]);
            cmax(ans, (r[i][j] + l[i][j] - 1) * u[i][j]);
        }

现在我们解决了最大矩形问题，那么最大正方形呢？很简单，因为最大正方形一定是最大矩形的子正方形。所以我们只需枚举所有悬线，计算每条悬线所对应矩形的最大子正方形面积：