前面的文字介绍了舞蹈链,这里就不详细描述什么是舞蹈链了,舞蹈链(Dancing links)是一种数据结构,可以用来实现X算法,以解决精确覆盖问题。本篇的内容主要把舞蹈链Dancing links应用于实际问题,通过实践才能帮助大家更好的理解,片面的了解理论知识,最终不能落到实处,也就没有意义了。
当然,把Dancing links应用于实际问题时,只有一个难点,就是如何把具体的问题转换为可以精确覆盖的01矩阵模型,一旦完成了这个步后,直接套用模板就可以解决问题了。
应用之一:伤脑筋十二块
伤脑筋十二块是Dancing links精确覆盖的典型应用,理解起来最容易
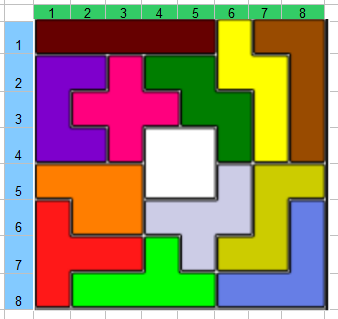
图1:12片5格骨牌的拼图
题目描述:
给你12个如上图的5格骨牌,如何让程序拼出如上的“口”字图形。
上图是题目的一个答案,你知道程序如何得到这个答案的吗?没错,就是用Dancing links的精确覆盖。
我们想象一个有72列的矩阵,其中12列是12个骨牌,剩下60列是60个非中心部分的格子。
所有可能的行来代表在一块骨牌在棋盘上得放置方案;每行有一些“1”,用来标识被覆盖的格子,5个1标识一个骨牌放置的位置(恰有1568个这样的行)
我们将最前面的12列命名为F,I,L,P,N,T,U,V,W,X,Y,Z,并且我们可以用两个数字i,j给矩阵中对应棋盘上的第i行第j列格子的那一列命名。通过给出那些出现了“1”的列的名字,可以很方便地表示每一行。
例如,图2就是与下面12行的对应的精确覆盖。

1568个行指的是12个骨牌可放置方案的总和,比如长条骨牌I共有64种放置方案,1568中就包含了这64种 这1568行中,每行都有6个1,分布在72个列中
这个矩阵的构造思路是:
首先找约束关系,这里只有两个约束关系,
(1)12个骨牌,每种只有1个;
(2)60个空格中,一个位置只能放一种骨牌(否则就要重叠着放了);
因为第一个约束关系,有了12个列来区分骨牌种类,因为第二个约束关系,有了60个选5个来表示骨牌放置 。
应用之二:数独问题 sudoku
解数独,生成数独,都可以使用精确覆盖,要把数独问题构造成01矩阵还是有一定的难度。
首先找约束关系,这里只有四个约束关系,
(1)81个格子中每个格子只能放一个数字
(2)每一行的数字不能重复
(3)每一列的数字不能重复
(4)每一九宫内的数字不能重复
![]()
四个约束关系中,每个约束对应一个列域,对于第二个约束关系,数独中共有9行,每行可以填9个不同的数字;
因此第二个列域,共有9* 9,81个列,依此类推,数独问题共有列324个;
由于81个格子,每个格子都最多有9种选择,所以行最多有81*9=729行;
这样01矩阵的每行都有4个1,第一个1分布在1到81列,第二个1分布在82到162列,第三个1分布在163到243列;
最后一个1分布在其余列区域。
思考:为什么不能这样构造01矩阵,用5个1,第一个1表示格子序号,有81个列,第二个1表示数字,从1到9有9个列,第三个1表示行号,有9行,第四个1表示列号也有9个,第五个1表示九宫格序号,也有9个,这样共有117列。
为了便于理解,举个例子
9,2,0,0,0,0,0,0,0,
5,0,0,8,7,0,0,0,0,
0,3,8,0,9,1,0,0,0,
0,5,2,9,3,0,1,6,0,
0,9,0,0,0,0,0,3,0,
0,7,3,0,6,4,9,8,0,
0,0,0,4,1,0,2,5,0,
0,0,0,0,5,3,0,0,1,
0,0,0,0,0,0,0,7,3
如上数独有空格40个,已知格子41个,把这个数独构造成01矩阵,矩阵的行有40*9+41共401行。
对于第一个数字9,在1到81列的第一列,在82到162列的第9个,即90列,在163列到243列的第9个,在244到324列的第9个各占一个1 ;
对于第三个数字0,由于有9个选择,所以在构造01矩阵时,要向矩阵插入9个行,来表示各种可能;
对于第四个数字8,它在二行四列,把这个数字写入dancing link的网状数据结构时,需要新增四个节点,这四个节点都在同一行,它们的列序号分别为13, 81 + 9 + 8 - 1,81 + 81 + 3 * 9 + 8 - 1,81 + 81 + 81 + 9 + 8 - 1, 序号是从0开始的,所有要减去一。
现在假设,2行6列的空格是数字8,那么这个数字也会对应四个节点,列序号分别为15,81 + 9 + 8 - 1, 81 + 81 + 5 * 9 + 8 - 1, 81 + 81 + 81 + 9 + 8 - 1,
可以看到, 这两个8的行域,九宫格域都是相同的,表示这两个数字的行和九宫格都相冲了,四个列域,只要有一个相冲,两条记录就不能共存。这两个8显然不能共存。
数独还有一个变种,对角线数独,两条对角线的数字也不能重复,这时构造01矩阵模型时,就需要额外增加两个列域,左对角线域,右对角线域。增加的两个列域都只有9列,
对于1行1列的数字,会在01矩阵模型中对应5个节点,
对于2行3列的数字,由于不位于两条对角线上,会在01矩阵模型中只对应4个节点,
对于5行5列的数字,恰好在两条对角线的交汇处,会在01矩阵模型中对应6个节点
对于数独的生成
总体思路是一行一行的生成,第一行可以用一个随机的1到9的排列,接下来的8行,每行都要用dancinglink求解可行的排序
(1)先对1到9这9个数进行随机排列,把这个排列作为数独终盘布局的第一行
(2)自己写函数筛选出下一行,每个格子可以填写的数字集合,筛选时不用考虑行冲突
比如对于排列5,9,7,4,2,6,8,3,1
筛选结果如下:123468,123468,123468,135789,135789,135789,245679,245679,245679
表示对于下一行的1,2,3列,可以选择的数字集合有1,2,3,4,6,8.
下一行的4,5,6列,可以选择的数字集合有1,3,5,7,8,9
下一行的7,8,9列,可以选择的数字集合有2,4,5,6,7,9
这时,构造01矩阵,就只有2个约束关系
(1)对于下一行的9个格子,每个格子只能放一个数字
(2)对于下一行的9个格子中的数字,每个数字都不能重复
因为第3个和4个约束,已经在筛选时考虑进去,这里不需再多此一举
这时的01矩阵,列有9+ 9=18个,行有6* 9 = 54行(6+6+6+6+6+6+6+6+6)。
应用之三:N皇后
N皇后问题也可以转换为Dancing links的精确覆盖问题,这里只讲如何把n皇后问题转换为01矩阵,首先有四个约束关系
(1)所有皇后不能在同一行
(2)所有皇后不能在同一列
(3)所有皇后不能在同一左斜线
(4)所有皇后不能在同一右斜线
为了便于理解,举个例子:n=8时,有8行,8列,15个左斜线,15个右斜线(2*n-1),这样构造的矩阵有46个列,8*8=64个行,矩阵的每行都有4个1,分别分布在行域,列域,左斜线域,右斜线域,在编程求解这个问题时,需要做一点变通,因为左斜线域,右斜线域的列不可能被全部覆盖,因此只需行域和列域被完全覆盖就算找到问题的一个解了。
附:
dancing LInks 求解数独的C++代码
#include<iostream>
#include<string.h>
using namespace std;
struct Node
{
Node *up;
Node *down;
Node *left;
Node *right;
Node *colRoot; //列首
int row; //所在行
int sum; //此列节点总数
};
#define R 729
#define C 324
class Dlx
{
public:
Node *nodes,*row,*col,*head;//可用节点,行首,列首,总头节点
int rowNum,colNum,nodeCount;//行数,列数,总节点数
int *result,resultCount;//结果,结果行数
Dlx()
{
nodes=new Node[R*C];//直接用数组竟然运行不起,栈溢出了,还得放在堆里
row=new Node[R];
col=new Node[C+1];
result=new int[R];
}
~Dlx()
{
delete []nodes;
delete []row;
delete []col;
delete []result;
}
void init(int r,int c);//初始化
void cover(Node *t);//覆盖一列
void uncover(Node *t);//取消覆盖
bool solove(int k=0);//搜索出结果
void addNode(int r,int c);//添加一个节点
};
void Dlx::init(int r,int c)
{
int i;
rowNum=r;
colNum=c;
//将各列连起来,col[colNum]为总头节点
for(i=0;i<=colNum;i++)
{
col[i].up=col[i].down=col+i;
col[i].left=col + (i+colNum)%(1+colNum);
col[i].right=col + (i+1)%(1+colNum);
col[i].sum=0;
}
head=col+colNum;
//将各行节点数清零
for(i=0;i<rowNum;i++)
{
row[i].up=row[i].down=row[i].left=row[i].right=row[i].colRoot=row+i;
}
nodeCount=0;//总节点数清零
}
void Dlx::addNode(int r,int c)
{
nodes[nodeCount].up=col[c].up;
nodes[nodeCount].down=col+c;
nodes[nodeCount].left=row[r].left;
nodes[nodeCount].right=row+r;
nodes[nodeCount].row=r;
nodes[nodeCount].colRoot=col+c;
col[c].up=col[c].up->down=row[r].left=row[r].left->right=nodes+nodeCount++;
col[c].sum++;
}
void Dlx::cover(Node *t)
{
Node *p,*q;
t->left->right=t->right;
t->right->left=t->left;
for(p=t->down;p!=t;p=p->down)
{
for(q=p->right;q!=p;q=q->right)
{
q->up->down=q->down;
q->down->up=q->up;
q->colRoot->sum--;
}
}
}
void Dlx::uncover(Node *t)
{
Node *p,*q;
for(p=t->up;p!=t;p=p->up)
{
for(q=p->left;q!=p;q=q->left)
{
q->up->down=q->down->up=q;
q->colRoot->sum++;
}
}
t->left->right=t->right->left=t;
}
bool Dlx::solove(int k)
{
//是否还有未覆盖的列
if(head->right==head)
{
//记录完成覆盖所用行数
resultCount=k;
return true;
}
Node *pMin,*p,*q;
//找到节点数最少的一列,并覆盖
for(pMin=head->right,p=pMin->right;p!=head;p=p->right)
{
if(pMin->sum>p->sum)
pMin=p;
}
cover(pMin);
for(p=pMin->down;p!=pMin;p=p->down)
{
result[k]=p->row;
//选定此列上的一个节点,将此节点所在行上所有节点的对应列进行覆盖
for(q=p->right;q!=p;q=q->right)
cover(q->colRoot);
if(solove(k+1))
return true;
//如果不能成功,则取消覆盖
for(q=p->left;q!=p;q=q->left)
uncover(q->colRoot);
}
uncover(pMin);
return false;
}
int getRowIndex(int rowNum)
{
int num = rowNum%9;
int rowIndex = rowNum / 81;
return 81 + rowIndex*9 + num;
}
int getColIndex(int rowNum)
{
int num = rowNum%9;
int index = rowNum/9; //位置
int colIndex = index%9;
return 162 + colIndex*9+num;
}
int getSquareIndex(int rowNum)
{
int num = rowNum%9;
int index = rowNum/9; //位置
int rowIndex = index / 9;
int colIndex = index%9;
int squareIndex = int(rowIndex/3)*3 + colIndex/3;
return 243 + squareIndex*9+num;
}
int main3()
{
int i,j;
int node4=0;
char str[82];
Dlx dlx;
//cin>>n;
dlx.init(729,324);
//for(i=0;i<9;i++)
//{
// cin>> (str+i*9);
//}
//......52..8.4......3...9...5.1...6..2..7........3.....6...1..........7.4.......3.
const char *input = ".2738..1..1...6735.......293.5692.8...........6.1745.364.......9518...7..8..6534.";
strcpy(str,input);
for(i=0;i<729;i++)
{
//cout << "row=>" << i << "\tcol=> 位置" << i/9 <<"\t行"<<81+i/9/9*9+i%9<<"\t列"<<162+i/9%9*9+i%9<<"\t块"<< 243+(i/9/9/3*3+i/9%9/3)*9+i%9;
//cout << "row=>" << i << "\tcol=> 位置" << i/9 <<"\t行"<<getRowIndex(i)<<"\t列"<<getColIndex(i)<<"\t块"<<getSquareIndex(i);
if(str[i/9]=='.' || str[i/9]-'1'==i%9)
{
node4++;
int rowIndex = i;
int colIndex = i/9;
dlx.addNode(rowIndex,colIndex);//位置冲突
dlx.addNode(rowIndex,getRowIndex(i));//行冲突
dlx.addNode(rowIndex,getColIndex(i));//列冲突
dlx.addNode(rowIndex,getSquareIndex(i));//块冲突
// cout << "\t<=";
}
//cout << endl;
}
if(dlx.solove())
{
//结果存到字符串中
for(i=0;i<81;i++)
{
j=dlx.result[i];
str[j/9]='1'+j%9;
}
//输出字符串
for(i=0;i<9;i++)
{
for(j=0;j<9;j++)
cout<<str[i*9+j];
cout<<endl;
}
}
return 0;
}
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程