什么是记忆化搜索?记忆化搜索在本质上,还是动态规划,只是实现方式采用了深度优先搜索的形式,但是它不像深度优先搜索那样重复枚举所有情况,而是把已经计算的子问题保存下来,这样就和动态规划的思想不谋而合了。
本篇文章会通过最简单的例子对记忆化搜索进行深入讲解,帮助大家学会什么是记忆化搜索。
一、记忆化搜索
记忆化搜索是一种搜索的形式,对搜索的结果用数组或其他数据结构记录下来。若当前状态搜索过了,则返回已存储的答案。这样,每个状态最多计算1次。
我们以斐波那契数列为例,用递归实现的fib数组计算代码是这样的:
int fib(int xn){
if(n==1||n==2){
return 1;
}
return fib(n-1)+fib(n-2);
}搜索树是长这样的
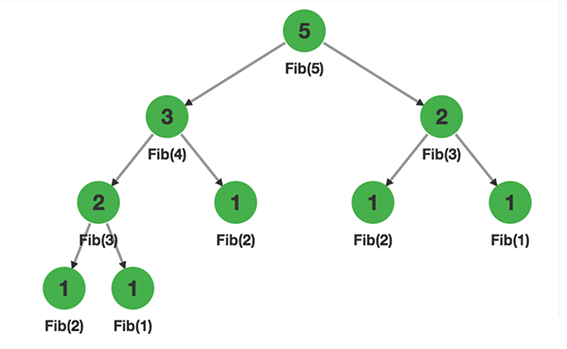
我们可以发现,为了求Fib(5),会先求Fib(4),然后求出Fib(3),在求Fib(4)的时候,实际上已经把Fib(3)求出来了,而求Fib(5),又计算了一次,这些计算是多余的,因为不管在任何情况下计算出的Fib(3),结果都一模一样。
所以,我们求出Fib(x)后,用一个数组F[x]来记录这个数,如果以后需要Fib(x)的值,直接从数组中取出就可以了。
代码如下:
#include <iostream>
using namespace std;
const int mod = 1000000009;
int f[10000];
int fib(int x) {
if(f[x]){
return f[x];
}
if (x <= 2) {
return f[x]=1;
}
else {
return f[x]=(fib(x - 1) + fib(x - 2))%mod;
}
}
int main() {
int n;
cin >> n;
cout << fib(n) << endl;
return 0;
}二、记忆化搜索与动态规划
相比较于记忆化搜索,动态规划一般要遍历所有的状态,神之包括一些不可行的状态,而记忆化搜索可以进行剪枝包括可行性剪枝、最优性剪枝等,避免了一些多余的计算。
记忆化搜索的程序思路好想但容易写错,通常代码要短一些。
对比如下:
| 记忆化搜索 | 动态规划 | |
| 动态规划 | < | |
| 时间复杂度 | = | |
| 运行效率 | ≥ | |
| 思维速度 | ≤ | |
| 实现难度 | ≥ | |
| 计算难度 | 自顶向下 | 自底向上 |
| 解决范围 | > | |
| 通常,一道动态规划算法能解决的问题,也可以用记忆化搜索的方式解决;但能有记忆化搜索解决的问题却不一定能用动态规划的多重循环方式解决。 | ||
| 记忆化搜索的本质就是将深度优先搜索的过程,通过避免重复计算同一个状态的结果,从而将时间复杂度优化到多项式复杂度。 |
三、滑雪问题(记忆化搜索)
XXX喜欢滑雪,这并不奇怪, 因为滑雪的确很刺激。可是为了获得速度,滑的区域必须向下倾斜,而且当你滑到坡底,你不得不再次走上坡或者等待YYY来载你。XXX想知道载一个区域中最长的滑坡。
区域由一个二维数组给出。数组的每个数字代表点的高度。下面是一个例子:
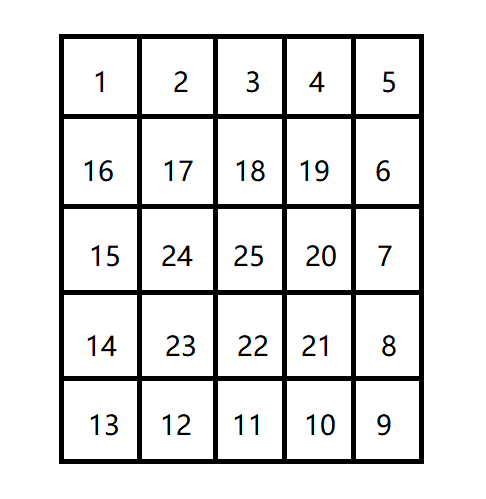
XXX可以从某个点滑向上下左右相邻四个点之一,当且仅当高度减小。在上面的例子中,一条可滑行的滑坡为24-17-16-1。当然25-24-23-…-3-2-1更长。事实上,这是最长的一条。
【输入格式】
输入的第一行表示区域的行数R和列数C(1 <= R,C <= 500)。下面是R行,每行有C个整数,代表高度h,0<=h<=10000。
【输出格式】
输出最长区域的长度。
【输入输出样例 1】
input
5 5 1 2 3 4 5 16 17 18 19 6 15 24 25 20 7 14 23 22 21 8 13 12 11 10 9
output
25
时间限制:2s
空间限制:128MB
题解:
本题的测试数据有着一定的误导性,有些人在开始会直接出现两个错误思路:
(1)从单个或多个最高点开始的路径一定最长
(2)每次选择与当前点落差最小的点作为下一个点的路径一定最长
(3)前两种思路全部出现
这三种情况实际上只要稍稍想一想就能发现反例,就看你能否仔细思考反问了
正解:记忆化搜索
爆搜思路:将每个点作为起始点,向四个方向中合法的点试最长路径,这样有多层嵌套循环的题目,单纯的爆搜基本上都会爆时间 有空可以算一下,所以需要在DFS时带上记忆化,用全局数组记录每个点自身为起始点时的最长路径,需要时直接取用,更详细请看下面代码与注释
#include<bits/stdc++.h>
using namespace std;
typedef struct node
{
int h,path;//h:此点的高度,path:以该点为起始点时的最长路径
}NODE,*PNODE;
NODE a[501][501];
int dx[]={0,1,0,-1},dy[]={1,0,-1,0},n,m;
int calc(int x,int y)
{
if(a[x][y].path)
return a[x][y].path;//如果已经有了路径,直接返回即可,非常省时
int i,x1,y1,maxx=0,t;
for(i=0;i<4;i++)
{
x1=x+dx[i];
y1=y+dy[i];//下一个点
if(x1>0&&x1<=n&&y1>0&&y1<=m&&a[x1][y1].h<a[x][y].h)//判断下一个点是否合法,注意:只要是比当前点低的点都要进
{
t=calc(x1,y1);//继续递归计算
maxx=max(maxx,t);//更新最大路径
}
}
return a[x][y].path=maxx+1;//这里处理的稍微简洁了一点
}
int main()
{
int i,j,t,ans=0;
scanf("%d %d",&n,&m);
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
scanf("%d",&a[i][j].h);//接收数据
for(i=1;i<=n;i++)
for(j=1;j<=m;j++)
{
t=calc(i,j);
ans=max(ans,t);
}
printf("%d",ans);
return 0;
}C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程