傅里叶-莫茨金消元法的应用

傅里叶 - 莫茨金消元法的英文名：Fourier-Motzkin Elimination，简称 FME 算法，它是一种用于从线性不等式中消除变量的数学方法。

它的命名源自于在 1827 年和 1936 年独立发现该算法的 Joseph Fourier 和 Theodore Motzkin 的姓氏。

1. 展示

从线性不等式中消除一组变量，是指通过将关系式中的若干个元素有限次地变换，消去其中的某些元素，从而解决问题的一种方法。

如果线性不等式中的所有变量都被消除，那么我们会得到一个常不等式。因为当且仅当原不等式有解时，消元后的不等式才为真，消除所有变量可用于检测不等式系统是否有解。

考虑一个含 n 个不等式的系统S，有从到的r个变量，其中为要消除的变量。根据系数的符号（正、负或空）， S中的线性不等式可以分为三类：

（1）形式为的不等式，对于范围从 1 到 （ 为这种不等式的数量）的 j，用表示； 

（2）形式为的不等式，对于范围从 1 到 （ 为这种不等式的数量）的 j，用表示；

（3）不包含的不等式，设它们构成的不等式组为∅。

因此原系统等价于

消元包括产生一个等价于的系统。显然，这个公式等价于

不等式

等价于对于且，所有个不等式构成的不等式组。

因此，我们将原系统S转换为另一个消掉的系统，这个系统有个不等式。特别地，如果，那么新系统不等式的个数为。

2. 例题

考虑以下不等式系统：

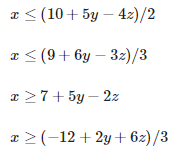
为了消除 x，我们可以根据 x 改写不等式：

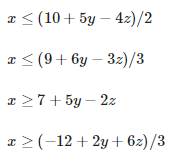
这样我们得到两个≤不等式和两个≥等式；如果每个≤不等式的右侧至少是每个≥不等式的右侧，则系统有一个解。我们有2X2这样的组合：

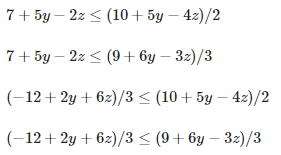
现在我们有了一个新的少了一个变量不等式系统。

3. 时间复杂度

在 n 个不等式上消元可以最多得到个不等式，因此连续运行 d 步可以得到最多的双指数复杂度。这是由于算法产生了许多不必要的约束（其他约束隐含的约束）。必要约束的数量以单一指数增长。

可以使用线性规划 (Linear Programming, LP) 检测不必要的约束。

4. 应用

信息论的可实现性证明保证了存在性能良好的编码方案的条件。这些条件通常使用线性不等式系统描述。系统的变量包括传输速率和附加辅助速率。通常，人们旨在仅根据问题的参数（即传输速率）来描述通信的基本限制，因此述辅助率需要消除上。而我们正是通过傅立叶 - 莫茨金消元法来做到这一点的。

5. 实现

在编程语言中，Racket，一种基于 Lisp 的多范式编程语言在 fme - Fourier-Motzkin Elimination for Integer Systems) 中对 FME 算法做了简单函数代数实现。