插头DP图文实例讲解

本篇通过图文解析讲述插头DP的内容，结合前面的状态压缩DP知识，以及前置知识：哈希，方便大家能快速理解。

在阐述什么是插头DP之前，我们先了解插头DP有什么用？插头DP是用来解决一类网格图上的连通性问题的强力工具。题目的特征是给定的网格非常小（这个特征类似状压DP）。事实上，插头DP也可以看做是状压DP的一种。

一、什么是插头DP

很显然，是一个关于插头的动态规划。那么，什么是插头呢？

如图我们在一个方格内，关于格点画一条闭合回路。

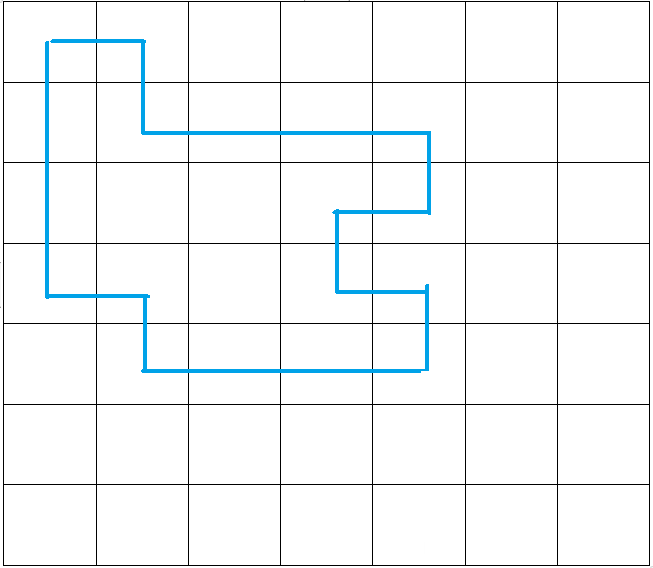
对于每一个方格，内部，有六种情况

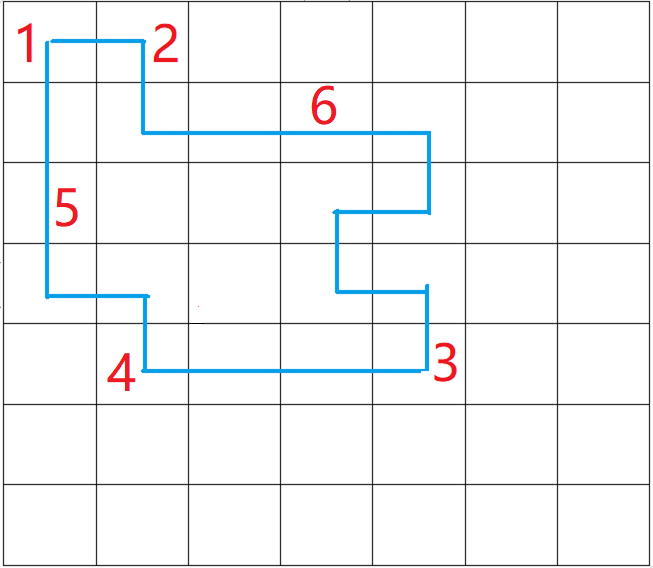
不难发现，对于回路里的任何一个方格，四条边中，有且仅有两个与表示路径的蓝色线相交。这也很好理解，进一次，出一次，C（4，2）=6。

我们现在把格子里的蓝色线条，变成从格子中心指向外边的→。

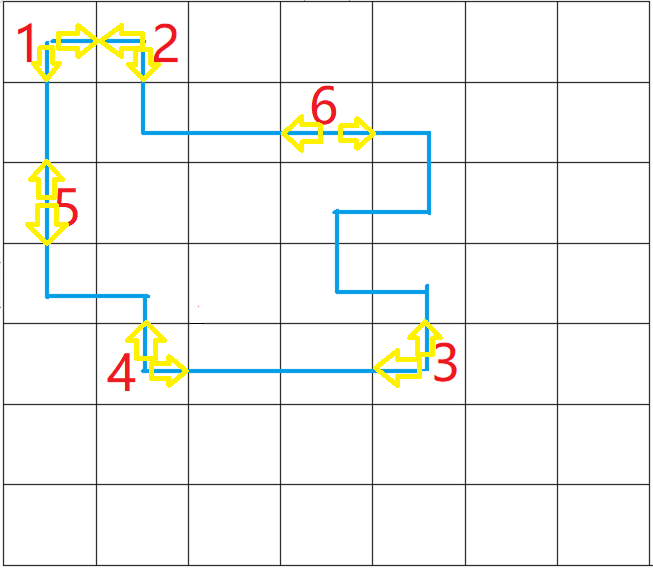
这个箭头，也就是所谓的插头。

二、例题

我们结合一个例题来看。

题目：给出n*m的方格，有些格子不能铺线，其它格子必须铺，可以形成多个闭合回路。问有多少种铺法？

输入格式

每个测试点多组数据

第一行一个正整数T，表示有T组数据

每组数据：

第1行，n,m(2<=n,m<=12)

从第2行到第n+1行，每行m个数字（1 or 0），1表铺线，0表不铺线

输出格式

每组数据输出一个整数（表方案数）

输入输出样例

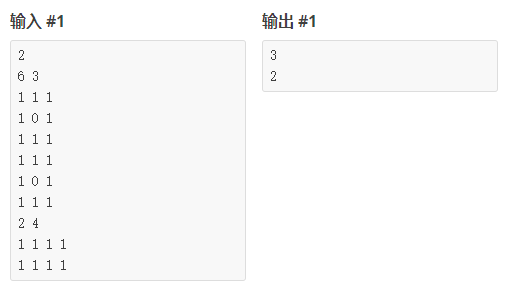
题目大意：给出n*m的方格，有些格子不能铺线，其它格子必须铺，可以形成多个闭合回路。问有多少种铺法？（1<=n,m<=12)

那么，把回路模型变成插头模型有什么好处或者性质呢？

1. 首先，我们可以发现，如果一个格子上方的格子有下插头，那这个格子一定有上插头。其它方向类似。

2. 按1的方法设置插头，最后一定会构成回路。

3. 一个格子的合理取法合且仅合相邻的格子有关。

观察下第三点，它其实代表了无后效性。假设我们从上到下，从左到右的处理每一个格子，那么我们只需要记录部分格子的状态即可，再往上的格子具体状态不用知道。

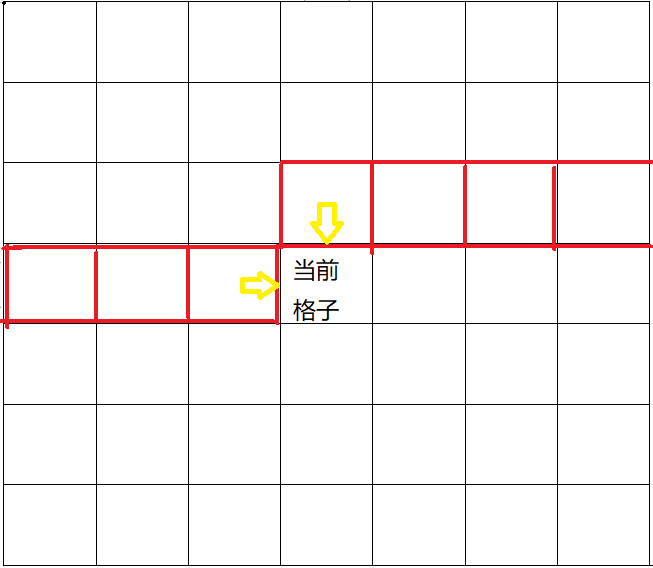
如上图，对于当前格子，我们只需要知道红色的这些格子就行了，再上面的格子具体的取法，已经不会对下面任何未处理的格子产生影响。

已经掌握了状态压缩的你，一定能轻松的算出状态总数，每个格子6种，维护n个格子。总共种状态，只有2e9个状态。

别急，我们真的需要2e9个状态嘛？这些格子里，指向彼此和已经处理过的格子的插头，显然是废物信息。我们实际上只需要知道这些插头嘛：

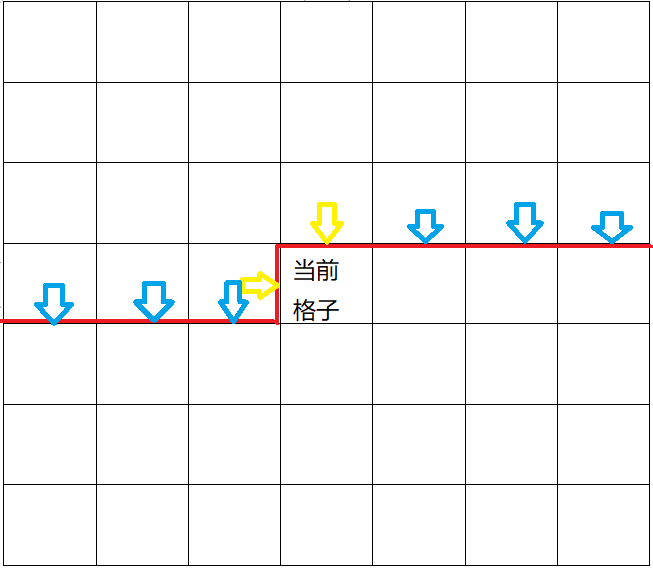
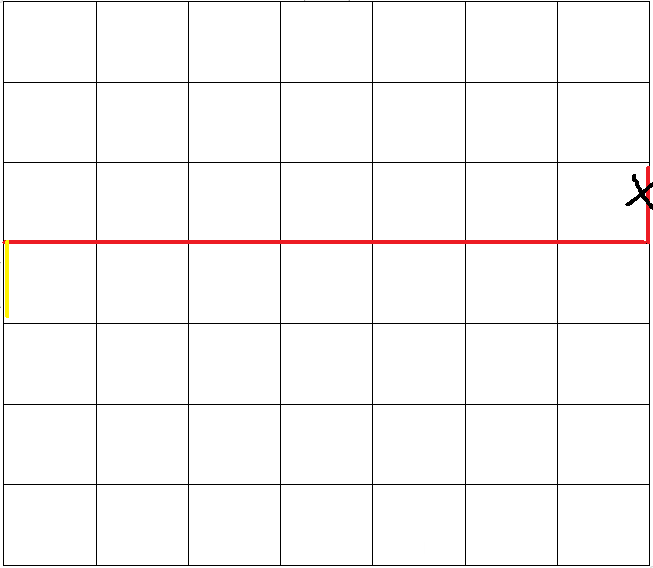
蓝色的是其它格子需要用到的，黄色的是当前格子需要用到的。我们叫红色的这个线为轮廓线。我们只需要知道这轮廓线上m+1个箭头是否存在就可以了。总共个状态。再乘上n和m，时空复杂度都绰绰有余。

那么，怎么实现呢？我们要解决两个问题。

1. 已知这些插头的情况下，这个方格该如何填。

2. 填完这个方格后，如何得到下一个方格所需要的插头状态，更特殊的，如何从上一行行末，变到下一行行初。

问题1：

0：若这个格子不能走，则不能存在左侧和上方插头。

1：如果当前格子存在左侧插头和上方插头，那么只有一种合理填法。

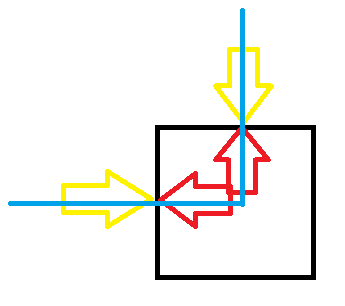
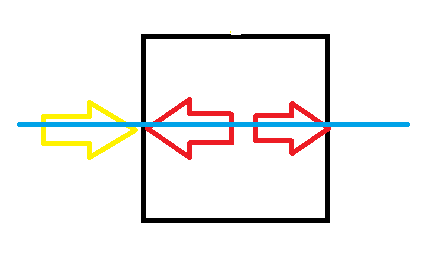
2：如果仅存在左侧插头，那么有两种合理填法。

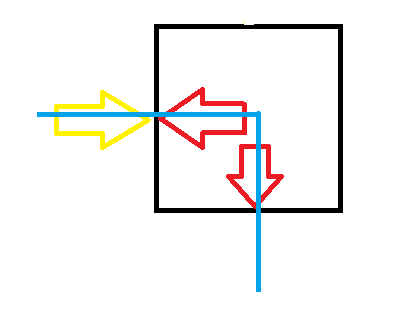
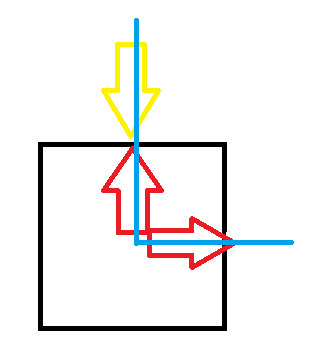
3：如果仅存在上方插头，那和上一种类似，也是两种填法。

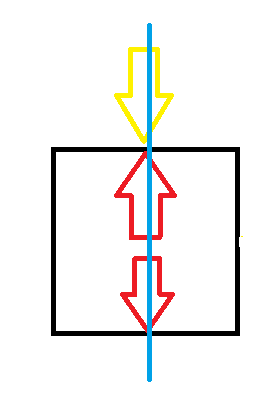
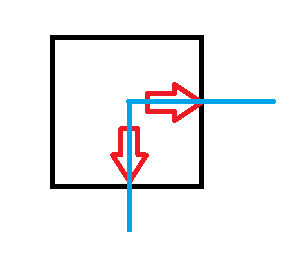
4：如果都不存在呢？只有一种填法

问题2：

解答了问题1，显然我们也得到了问题2的解答，毕竟我们填出了这个格子，自然知道插头分布。唯一特殊的是上一行末到这一行头的处理。上一行末不可能有右插头，那我们直接把上一行末状态的表示最后是否存在右插头的位置去掉，再添加一个表示没有左插头的位，不就表示出了这一行第一个的状态了嘛，为了方便写，下方的代码里，用dp[i][0][mask]表示转移后的上一行行末状态。

到这里，我们已经得到了解法了，成熟的评测机，应该自动AC了吧（划去）。

代码如下：

#include<iostream>
#include<stdio.h>
#include<cstring>
using namespace std;
int n,m,maxk,a[13][13];
long long dp[13][13][1<<14];
void init()
{ 
	scanf("%d%d",&n,&m);
	maxk=(1<<(m+1))-1;
	for (int i=1;i<=n;i++)
	{
		for (int j=1;j<=m;j++)
		{
			scanf("%d",&a[i][j]);
		}
	}
	memset(dp,0,sizeof(dp));
}
void solve()
{
	int prei,prej;
	dp[0][m][0]=1;
	for (int i=1;i<=n;i++)
	{
		for (int k=0;k<=maxk;k++)
		{
			dp[i][0][k<<1]=dp[i-1][m][k];
		}
		for (int j=1;j<=m;j++)
		{
			prei=i;
			prej=j-1;
			for (int k=0;k<=maxk;k++)
			{
				int b1=(k>>(j-1))&1;
				int b2=(k>>j)&1;
				if (!a[i][j])
				{
					if (!b1&&!b2) dp[i][j][k]+=dp[prei][prej][k];
				}
				else if (!b1&&!b2)
				{
					dp[i][j][k+(1<<j)+(1<<(j-1))]+=dp[prei][prej][k];
				}
				else if (b1&&!b2)
				{
					dp[i][j][k]+=dp[prei][prej][k];
					dp[i][j][k+(1<<(j-1))]+=dp[prei][prej][k];
				}
				else if (!b1&&b2)
				{
					dp[i][j][k]+=dp[prei][prej][k];
					dp[i][j][k-(1<<(j-1))]+=dp[prei][prej][k];
				}
				else if (b1&&b2)
				{
					dp[i][j][k-(1<<j)-(1<<(j-1))]+=dp[prei][prej][k];
				}
			}
		}
	}
	printf("%lld\n",dp[n][m][0]);
}
int main()
{
	int t;
	scanf("%d",&t);
	while (t--)
	{
		init();
		solve();
	}
	return 0;
}