什么是Lyndon分解？

我们定义一个串是Lyndon串，当且仅当这个串的最小后缀就是这个串本身。该命题等价于这个串是它的所有循环表示中字典序最小的。

引理 1：如果u和v都是Lyndon串并且u<v，则uv也是Lyndon串。

证明：

1、若len(u)≥len(v)

这时，u和v这两个串在len(v) 之前就出现了不同的字符，所以有v>uv，又因为v是Lyndon串，所以v的所有后缀都大于v，所以uv的所有后缀都大于uv，故uv 是Lyndon串。

2、若 len(u)<len(v)

若u不是v的前缀，那么有v>uv，得证。

若u是v的前缀，那么如果v<uv，则必有v[len(u)+1:]<v（也就是各自去掉了前∣u∣个字符），矛盾。

我们定义一个串S的Lyndon分解为一个字符串序列，满足：

，满足是Lyndon串。

，满足。

可以证明这种划分存在且唯一。

存在性证明

初始令m=∣S∣并且，然后每次不断找到并且合并为一个串。最后一定能使得所有的

唯一性证明

假设对于字符串S存在两个Lyndon 分解：

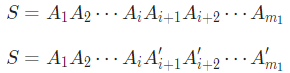
不妨设

观察在第二种分解中的对应情况。假设

那么由Lyndon串的性质可知：

矛盾。

引理2：若字符串v和字符c满足vc是某个Lyndon串的前缀，则对于字符d>c有vd是Lyndon串。

证明：

设该Lyndon串为v+c+t。

则，也就是说。

所以。

同时因为c>v[1]，我们有d>c>v[1]。

故v+d是一个Lyndon串。

Duval 算法

这个算法可以在O(n)时间复杂度，O(1)空间复杂度内求出一个串的Lyndon分解。

该算法中我们仅需维护三个变量i,j,k。

维持一个循环不变式：

是固定下来的分解，也就是，是Lyndon 串且。

是没有固定的分解，满足t是Lyndon串，且v是t的可为空的不等于t的前缀，且有

如下图：

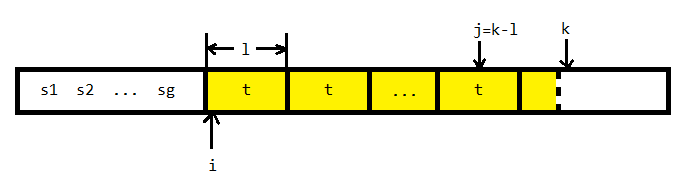
当前读入的字符是s[k]，令j=k−∣t∣。

分三种情况讨论：

当s[k]=s[j] 时，直接k←k+1，j←j+1，周期k-j继续保持

当s[k]>s[j] 时，由引理2可知v+s[k] 是Lyndon串，由于Lyndon分解需要满足，所以不断向前合并，最终整个形成了一个新的Lyndon串。

当s[k]<s[j] 时，的分解被固定下来，算法从v的开头处重新开始。

复杂度分析：i只会单调往右移动，同时k每次移动的距离不会超过i移动的距离，所以时间复杂度是O(n)的。

代码如下：

#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
char s[5000005];
int n,ans;
int main()
{
    scanf("%s",s+1);
    n=(int)strlen(s+1);
    for(int i=1;i<=n;)
    {
        int j=i,k=i+1;//初始化
        while(k<=n&&s[j]<=s[k])
        {
            if(s[j]<s[k])j=i;//合并为一整个
            else j++;//保持循环不变式
            k++;
        }
        while(i<=j)//从v的开头重新开始
        {
            ans^=i+k-j-1;
            i+=k-j;
        }
    }
    printf("%d\n",ans);
    return 0;
}