本篇将简要介绍α-β剪枝,这是一种基于剪枝( α-βcut-off)的深度优先搜索(depth-first search)。
一、什么是α剪枝?
(1)将走棋方定为MAX方,因为它选择着法时总是对其子节点的评估值取极大值,即选择对自己最为有利的着法;
(2)将应对方定为MIN方,因为它走棋时需要对其子节点的评估值取极小值,即选择对走棋方最为不利的、最有钳制作用的着法。
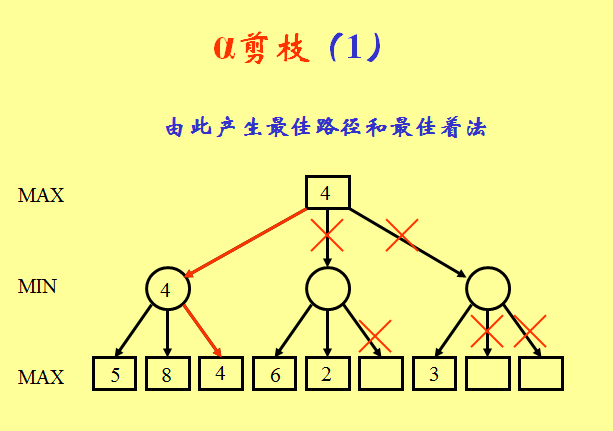
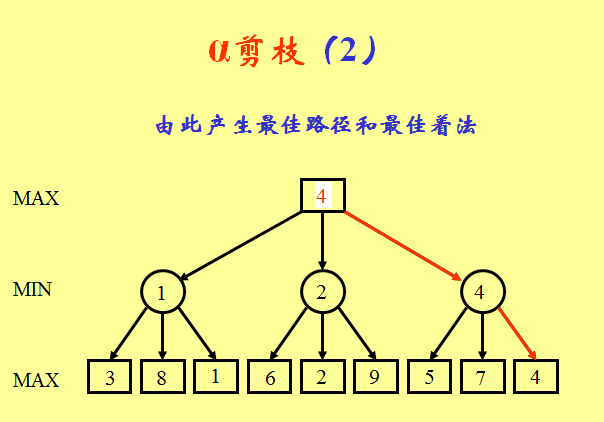
(3)在对博弈树(博弈树是指由于动态博弈参与者的行动有先后次序,因此可以依次将参与者的行动展开成一个树状图形。)采取深度优先的搜索策略时,从左路分枝的叶节点倒推得到某一层MAX节点的值,可表示到此为止得以“落实”的着法最佳值,记为α。
(4)显然此值可作为MAX方着法指标的下界。
(5)在搜索此MAX节点的其它子节点,即探讨另一着法时,如果发现一个回合(2步棋)之后评估值变差,即孙节点评估值低于下界α值,则便可以剪掉此枝(以该子节点为根的子树),即不再考虑此“软着”的延伸。
此类剪枝称为α剪枝。
二、什么是β剪枝?
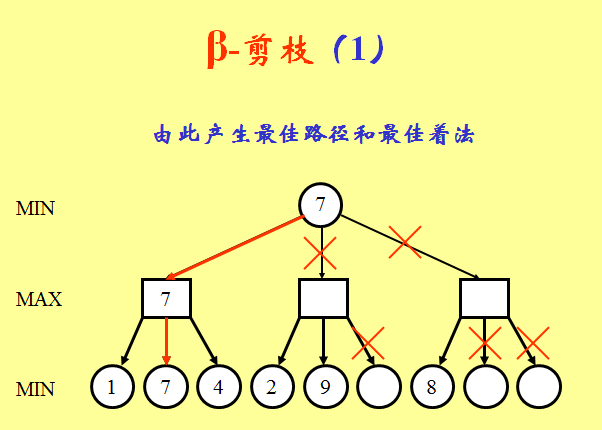
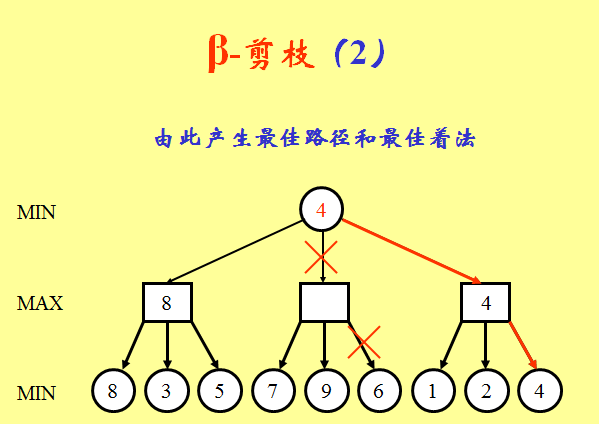
(1)同理,由左路分枝的叶节点倒推得到某一层MIN节点的值,可表示到此为止对方着法的钳制值,记为β。
(2)显然此β值可作为MAX方无法实现着法指标的上界。
(3)在搜索该MIN节点的其它子节点,即探讨另外着法时,如果发现一个回合之后钳制局面减弱,即孙节点评估值高于上界β值,则便可以剪掉此枝,即不再考虑此“软着”的延伸。
此类剪枝称为β剪枝。
三、什么是α-β剪枝?
α-β剪枝是根据极大-极小搜索规则的进行的,虽然它没有遍历某些子树的大量节点,但它仍不失为穷尽搜索的本性。
α-β剪枝原理中得知:
(1)α值可作为MAX方可实现着法指标的下界
(2)β值可作为MAX方无法实现着法指标的上界
(3)于是由α和β可以形成一个MAX方候选着法的窗口,也便出现了各种各样的α-β窗口搜索算法。
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程