复数的引入,追根求源,最初是为了求解没有实数根的二次方程。例如求解
![]()
这个由实数组成的方程,显然没有实数根。所以复数集可以看成实数集合的一个自然扩充。
首先引入一个“新数” i。使它满足
![]()
也就是说 i 是
![]()
的解。
我们再给复数定义:形如 z=a+bi的数就是复数。其中 a和b分别叫做复数 z 的实部和虚部。
注意,b才是虚部, bi不是虚部。
记作:a=Re(z),b=Im(z)
复数z=a+bi的分类
当虚部b=0时,复数z是实数;
当虚部b!=0时,复数z是虚数;
当虚部b!=0,且实部a=0时,复数z是纯虚数。
一些集合的记号
R——实数集,C——复数集
P——虚数集,Q——纯虚数集
有下列关系:
R∩P=ϕ
R∪P=C
Q⊊P⊊C
复数相等的充分必要条件
设两个复数分别为z1=a+bi,z2=c+di,而二者相等的充分必要条件是a=c而且b=d。
化虚为实是复数问题的通性通法
复数的运算法则
对于两个复数z1=a+bi,z2=c+di
z1+z2=(a+c)+(b+d)i
z1−z2=(a−c)+(b−d)i
z1×z2=(a+bi)(c+di)=(ac−bd)+(ad+bc)i
![]()
复数的运算定律
复数的加法满足交换律,结合律。
也就是z1+z2=z2+z1
(z1+z2)+z3=z1+(z2+z3)
复数的乘法满足交换律、结合律,以及乘法对于加法的分配律。也就是
z1×z2=z2×z1
(z1z2)z3=z1(z2z3)
z1(z2+z3)=z1z2+z1z3
共轭复数
当两个复数实部相等,虚部互为相反数时,就称其互为共轭复数。特别地,若复数的虚部不为零时,也称作互为共轭虚数。对于复数z=a+bi(a、b∈R),它的共轭复数![]() 用来表示。
用来表示。
共轭复数有如下基本性质
![]()
![]()
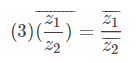
![]()
![]()
![]()
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程