简述旋转卡壳

1978年， M.I. Shamos's Ph.D. 的论文"Computational Geometry"标志着计算机科学的这一领域的诞生。当时他发表成果的是一个寻找凸多边形直径的一个非常简单的算法， 即根据多边形的一对点距离的最大值来确定。 

一、定义

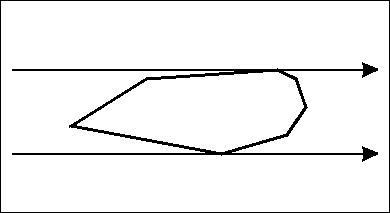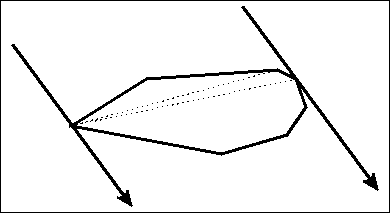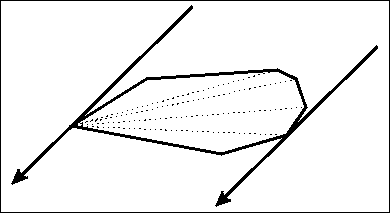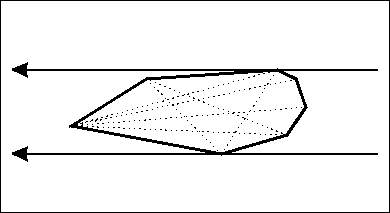
旋转卡壳算法在凸包算法的基础上，通过枚举凸包上某一条边的同时维护其他需要的点，能够在线性时间内求解如凸包直径、最小矩形覆盖等和凸包性质相关的问题。「旋转卡壳」是很形象的说法，因为根据我们枚举的边，可以从每个维护的点画出一条或平行或垂直的直线，为了确保对于当前枚举的边的最优性，我们的任务就是使这些直线能将凸包正好卡住。而边通常是按照向某一方向旋转的顺序来枚举，所以整个过程就是在边「旋转」，边「卡壳」。

二、应用

1. 计算距离

（1）凸多边形直径

（2）凸多边形宽

（3）凸多边形间最大距离

（4）凸多边形间最小距离

2. 外接矩形

（1）最小面积外接矩形

（2）最小周长外接矩形

3. 三角剖分

（1）洋葱三角剖分

（2）螺旋三角剖分

（3）四边形剖分

4. 凸多边形属性

（1）合并凸包

（2）找共切线

（3）凸多边形交

（4）临界切线

（5）凸多边形矢量和

5. 最薄截面

（1）最薄横截带

三、定理证明

1. 点集中最远的两个点一定出现在凸包的顶点上

证明：任取凸包内部两点，总能把连线延长至凸包边界处得到更远的两点，之后对于边界上的两点又可以移动到顶点处得到更远的两点。也就是说在求最大距离时凸包内部两点会被顶点两点覆盖掉。

2. 凸包直径 = 最大对踵点对距离 = 点集中两顶点最大距离

左半部分证明：凸包直径是距离最远的两条平行凸多边形切线，对踵点对是卡住凸多边形两侧切线的切点对。首先要知道在两切线旋转出最大距离时的对踵点对连线一定垂直两平行切线，若不垂直则旋转至垂直最优，若旋转至垂直后无法保证对踵点对不变则说明直径变大了，这与前提矛盾。之后可知凸包直径一定是某对对踵点对的距离，同时可以反证出其一定为最远的那对对踵点。

右半部分证明：同样用反证法，假设最远对踵点对不是距离最远的两点，那说明还存在距离更大的两点，垂直这两点连线作凸多边形两切线可得到更远的对踵点对，与前提矛盾。

3. 点集中构成面积最大的三角形时三个顶点一定出现在凸包的顶点上

证明：若三角形三个顶点在凸包内部则可以将顶点分别平移至凸包边界上，此时得到面积更大的三角形，之后任取一边为底边，可以把剩余的一个顶点平移至该边的切点位置，这样可以进一步扩大三角形面积，对每条边进行同样处理可以发现最终三个顶点都位于凸包顶点处。也就是说任意的凸包内部三角形都可以找到一个比它大的且顶点都在凸包顶点上的三角形来覆盖，因此得出结论。

4. 点集中构成面积最大的n边形时其n个顶点一定出现在凸包的顶点上

证明：由于要求面积最大，那么这个n边形一定是凸多边形，不会是凹多边形（凹多边形求凸包会得到面积更大边数更少的凸多边形），在凸包内部任取一个n边形都能把n个顶点平移至凸包边界上，之后类似上面那条结论的证明可以将n个顶点移动到凸包顶点位置来获得更大的n边形，得证。

5. 存在一对平行边的四边形其max(两条对角线长) > max(两斜边长)

证明：这是比较显然的，可以分两种情况+勾股定理证明。

6. 最小矩形覆盖一定有一条边与凸包上一条边重合

7. 凸包宽度 = 每条边到最远点距离的最小值

证明：首先要知道凸包宽度的定义，凸包宽度是任意两条平行切线距离的最小值，另外还有一个结论，对于任意的“点-点”的两条切线，总可以通过旋转得到距离更小的“点-边”切线或“边-边”切线。因此只需要枚举每条边，取所有边到其最远点距离的最小值。