欧拉图的判定

本篇将简要介绍欧拉图的概念、实现和应用，帮助大家在答题中更好的判定。

一、定义

圈：任选图中一个顶点为起点，沿着不重复的边，经过不重复的顶点为途径，之后又回到起点的闭合途径称为圈。

欧拉路径：通过图中所有边一次且仅一次遍历所有顶点的路径称为欧拉(Euler)路径；

欧拉回路：通过图中所有边一次且仅一次行遍所有顶点的回路称为欧拉回路；

欧拉图：具有欧拉回路的图称为欧拉图；

半欧拉图：有欧拉路径但没有欧拉回路的图称为半欧拉图。

欧拉图与半欧拉图的判定：

G是欧拉图 ⇔ G中所有顶点的度均为偶数 ⇔ G是若干个边不重的圈的并。

G是半欧拉图 ⇔ G中恰有两个奇数度顶点。

二、性质

欧拉图中所有顶点的度数都是偶数。

若G是欧拉图，则它为若干个环的并，且每条边被包含在奇数个环内。

三、判别法

1. 无向图是欧拉图当且仅当：

（1）非零度顶点是连通的

（2）顶点的度数都是偶数

2. 无向图是半欧拉图当且仅当：

（1）非零度顶点是连通的

（2）恰有 0 或 2 个奇度顶点

3. 有向图是欧拉图当且仅当：

（1）非零度顶点是强连通的

（2）每个顶点的入度和出度相等

4. 有向图是半欧拉图当且仅当：

（1）非零度顶点是弱连通的

（2）至多一个顶点的出度与入度之差为 1

（3）至多一个顶点的入度与出度之差为 1

（4）其他顶点的入度和出度相等

四、求欧拉回路或欧拉路

1. Fleury 算法

也称避桥法，是一个偏暴力的算法。

算法流程为每次选择下一条边的时候优先选择不是桥的边。

一个广泛使用但是错误的实现方式是先 Tarjan 预处理桥边，然后再 DFS 避免走桥。但是由于走图过程中边会被删去，一些非桥边会变为桥边导致错误。最简单的实现方法是每次删除一条边之后暴力跑一遍 Tarjan 找桥，时间复杂度是。复杂的实现方法要用到动态图等，实用价值不高。

2. Hierholzer 算法

也称逐步插入回路法。

（1）过程

算法流程为从一条回路开始，每次任取一条目前回路中的点，将其替换为一条简单回路，以此寻找到一条欧拉回路。如果从路开始的话，就可以寻找到一条欧拉路。

（2）实现

Hierholzer 算法的暴力实现如下：

（3）性质

这个算法的时间复杂度约为。实际上还有复杂度更低的实现方法，就是将找回路的 DFS 和 Hierholzer 算法的递归合并，边找回路边使用 Hierholzer 算法。

如果需要输出字典序最小的欧拉路或欧拉回路的话，因为需要将边排序，时间复杂度是（计数排序或者基数排序可以优化至）。如果不需要排序，时间复杂度是 。

（4）应用

有向欧拉图可用于计算机译码。

设有 m 个字母，希望构造一个有个扇形的圆盘，每个圆盘上放一个字母，使得圆盘上每连续 n 位对应长为 n 的符号串。转动一周（次）后得到由 m 个字母产生的长度为 n 的个各不相同的符号串。

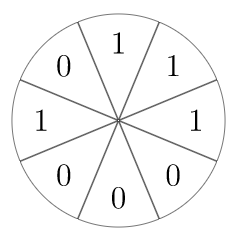
构造如下有向欧拉图：

设，构造D=<V，E> ，如下：

规定D中顶点与边的关联关系如下：

顶点引出 m 条边：。

边引入顶点。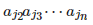

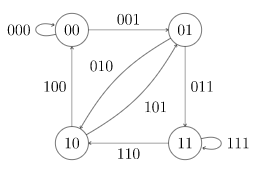
这样的D连通的，且每个顶点入度等于出度（均等于m），所以D是有向欧拉图。

任求D中一条欧拉回路C，取C中各边的最后一个字母，按各边在C中的顺序排成圆形放在圆盘上即可。