图的基础概念

图(Graph)是由顶点和连接顶点的边构成的离散结构。在计算机科学中，图是最灵活的数据结构之一，很多问题都可以使用图模型进行建模求解。

图(Graph)通常会放在树(Tree)后面介绍，树可以说是图的特例。

一、图的基础概念

图的结构很简单，就是由顶点 V 集和边 E 集构成，因此图可以表示成 G=(V, E) 。

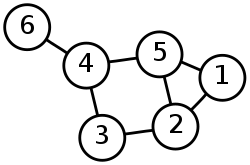
上图就是无向图，我们可以说这张图中，有点集 V=\{1, 2, 3, 4, 5, 6\} ，边集 E=\{(1, 2), (1, 5), (2, 3), (2, 5), (3, 4), (4, 5), (4, 6)\} 。在无向图中，边 (u, v) 和边 (v, u) 是一样的，简而言之，对称。

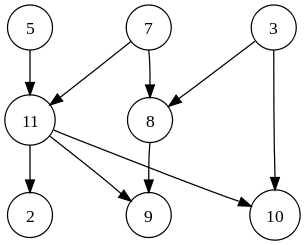
有向图也很好理解，就是加上了方向性，顶点 (u, v) 之间的关系和顶点 (v,u) 之间的关系不同，后者或许不存在。例如，地图应用中必须存储单行道的信息，避免给出错误的方向。

加权图：与加权图对应的就是无权图，也叫等权图。如果一张图不含权重信息，我们就认为边与边之间没有差别。不过，具体建模的时候，很多时候都需要有权重。

还有很多细化的概念，比如：无向图中，任意两个顶点间都有边，称为无向完全图；加权图起一个新名字，叫网(network)……等。

两个重要关系：

（1）邻接(adjacency)：邻接是两个顶点之间的一种关系。如果图包含 (u,v) ，则称顶点 v 与顶点 u 邻接。当然，在无向图中，这也意味着顶点 u 与顶点 v 邻接。

（2）关联(incidence)：关联是边和顶点之间的关系。在有向图中，边 (u,v) 从顶点 u 开始关联到 v ，或者相反，从 v 关联到 u 。注意，有向图中，边不一定是对称的，有去无回是完全有可能的。细化这个概念，就有了顶点的入度(in-degree)和出度(out-degree)。无向图中，顶点的度就是与顶点相关联的边的数目，没有入度和出度。在有向图中，顶点10有2个入度， 3\rightarrow10 ， 11\rightarrow10 ，但是没有从10指向其它顶点的边，因此顶点10的出度为0。

路径(path)：依次遍历顶点序列之间的边所形成的轨迹。注意，依次就意味着有序，先1后2和先2后1不一样。

简单路径：没有重复顶点的路径称为简单路径。也就是没有环。

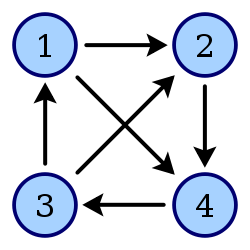
环：包含相同的顶点两次或者两次以上。图1-3中的顶点序列 <1,2,4,3,1> ，1出现了两次，当然还有其它的环，比如 <1,4,3,1> 。

无环图：没有环的图，其中，有向无环图有特殊的名称，叫做DAG(Directed Acyline Graph)（记住，DAG具有一些很好性质，比如很多动态规划的问题都可以转化成DAG中的最长路径、最短路径或者路径计数的问题）。

下面这个概念很重要：

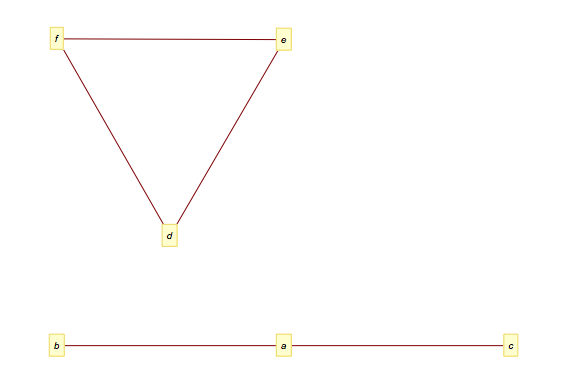
连通的：无向图中每一对不同的顶点之间都有路径。如果这个条件在有向图里也成立，那么就是强连通的。图1-4中的图不是连通的，我丝毫没有侮辱你智商的意思，我只是想和你说，这图是我画的，顶点标签有点小，应该看到a和d之间没有通路。

（1）连通分支：不连通的图是由2个或者2个以上的连通分支的并。这些不相交的连通子图称为图的连通分支。

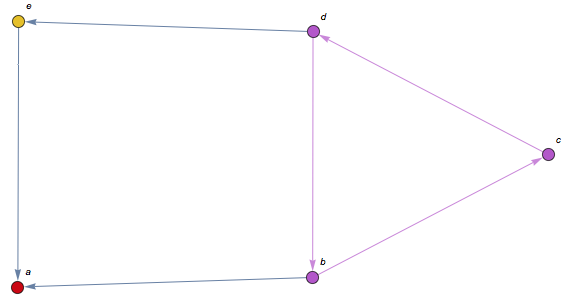
（2）有向图的连通分支：将有向图的方向忽略后，任何两个顶点之间总是存在路径，则该有向图是弱连通的。有向图的子图是强连通的，且不包含在更大的连通子图中，则可以称为图的强连通分支。图1-5中，a、e没有到\{b,c,d\}中的顶点的路径，所以各自是独立的连通分支。因此，图1-5中的图有三个强连通分支，用集合写出来就是：\{\{a\}, \{e\}, \{b, c, d\}\}（已经用不同颜色标出）。

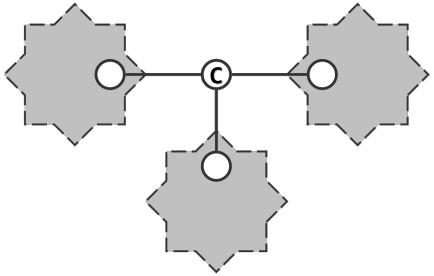
关节点(割点)：某些特定的顶点对于保持图或连通分支的连通性有特殊的重要意义。如果移除某个顶点将使图或者分支失去连通性，则称该顶点为关节点。如图中的c。

双连通图：不含任何关节点的图。

关节点的重要性不言而喻。如果你想要破坏互联网，你就应该找到它的关节点。同样，要防范敌人的攻击，首要保护的也应该是关节点。在资源总量有限的前提下，找出关节点并给予特别保障，是提高系统整体稳定性和鲁棒性的基本策略。

桥(割边)：和关节点类似，删除一条边，就产生比原图更多的连通分支的子图，这条边就称为割边或者桥。