一、什么是树
树是一种类似链表的数据结构,不过链表的结点是以线性方式简单地指向其后继指点,而树的一个结点可以指向许多个结点。树是一种典型的非线性结构。树结构是表达具有层次特性的图结构的一种方法。
二、相关术语
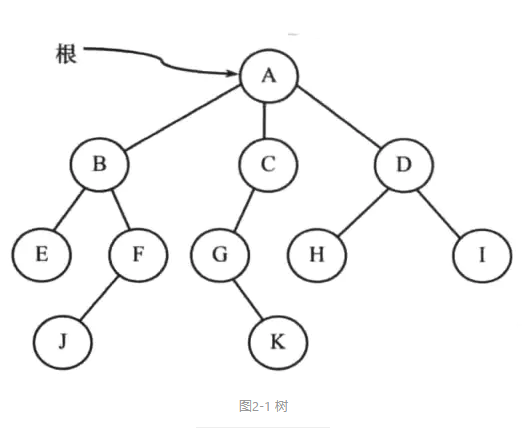
● 根结点:根结点就是一个没有双亲结点的结点。一棵树中最多有一个根结点(如图2-1的结点A就是根结点)。
● 边:边表示从双亲结点到孩子结点的链接(如图2-1的所有链接)。
● 叶子结点:没有孩子结点的结点叫做叶子结点(如图2-1中的E、J、K、H、I )。
● 兄弟结点:拥有相同的双亲结点的所有孩子结点叫做兄弟结点(如图2-1中的B、C、D是A的兄弟结点)。
● 祖先结点:如果存在一条从根结点到q的路径,且结点p出现在这条路径上,那么就可以把p叫做q的祖先结点(如图2-1中A、C、G是K的祖先结点)。
● 结点的大小:结点的大小是指子孙的个数,包括其自身(如图2-1中子树C的大小为3)。
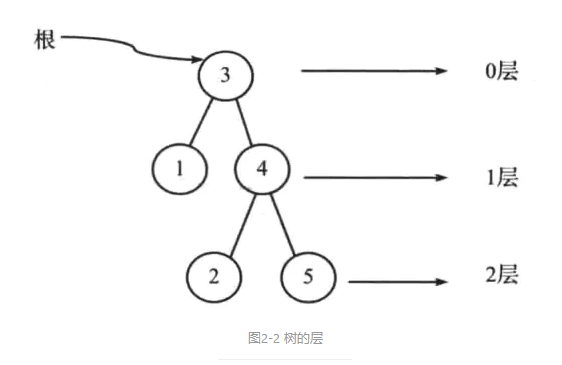
● 树的层:位于相同深度的所有结点的集合叫做树的层(如图2-2中的1和4具有相同的层)。
● 结点的深度:是指从根结点到该结点的路径长度(如图2-2中的5深度为2,3-4-5)。
● 结点的高度:是指从结点到最深结点的路径长度。树的高度是指根结点到树中最深结点的路径长度。只含有根结点的树的高度是0(如图2-2树的高度为2)。
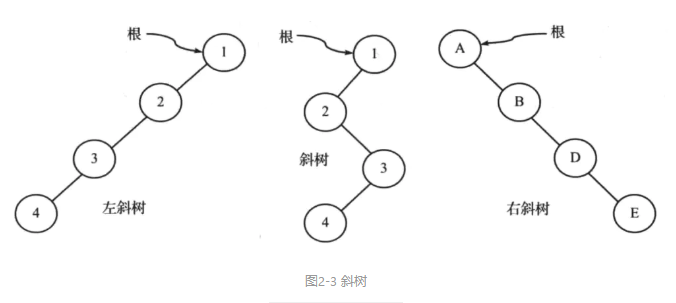
● 斜树:如果树中除了叶子结点外,其余每个结点都只有一个孩子结点,则这种树称为斜树(如图2-3)。
三、二叉树
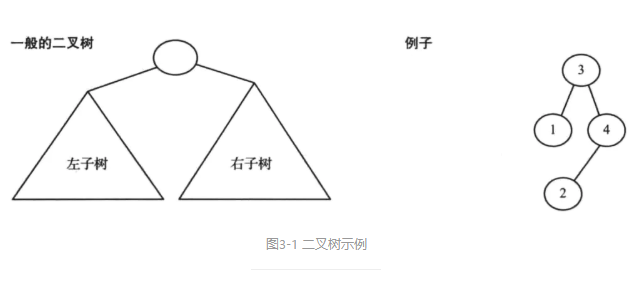
如果一棵树中的每个结点有0、1或2个孩子结点,那么这个树就称为二叉树。空树也是一棵有效的二叉树。一棵二叉树可以看作由根结点和两棵不相交的子树组成,如图3-1所示。
1. 二叉树的类型
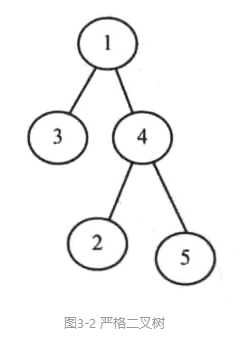
(1)严格二叉树:二叉树中的每个结点要么有两个孩子结点,要么没有孩子结点(如图3-2所示)。
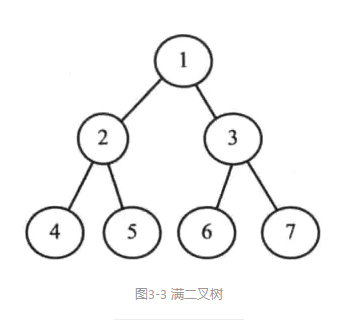
(2)满二叉树:二叉树的每个结点恰好有两个孩子结点且所有叶子结点在同一层(如图3-3所示)。
(3)完全二叉树:假定二叉树的高度为h。对于完全二叉树,如果将所有结点从根结点开始从左至右,从上至下,依次编号(假定根结点编号为1),那么将得到从1~n(n为结点总数)的完整序列。如果所有叶子结点的深度为h或者h-1,且结点在编号过程中没有漏掉任何数字,那么就叫做完全二叉树(如图3-4所示)。

2. 二叉树的性质
假定树的高度为h,且根结点的深度为0。
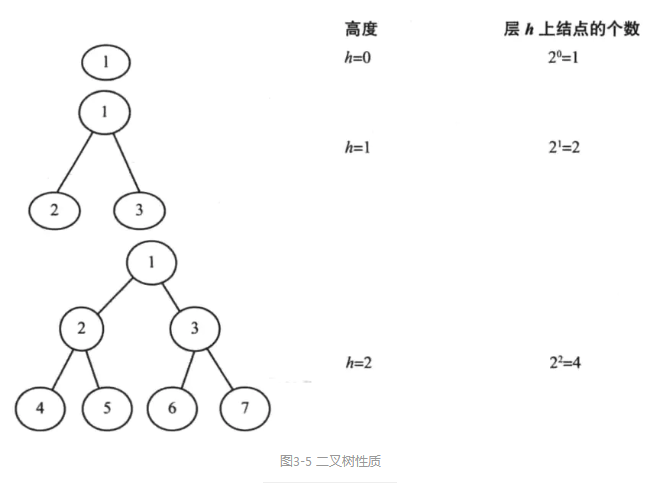
从图3-5可得出如下性质:
(1)满二叉树的结点个数n为[2^(h+1)] -1。因为该树总共有h层,每一层结点都是满的。
(2)满二叉树的叶子结点个数是2^h。
3. 二叉树的结构
表示一个结点的方法之一是定义两个指针,一个指向左孩子结点,另一个指向右孩子结点,中间为数据字段(如图3-6所示)。

代码实现:
public class BinaryTreeNode {
private int data;
private BinaryTreeNode left;
private BinaryTreeNode right;
public int getData(){
return data;
}
public void setData(int data) {
this.data = data;
}
public BinaryTreeNode getLeft() {
return left;
}
public void setLeft(BinaryTreeNode left) {
this.left = left;
}
public BinaryTreeNode getRight() {
return right;
}
public void setRight(BinaryTreeNode right) {
this.right = right;
}}4. 二叉树的遍历
访问树中所有结点的过程叫做遍历,遍历的目标是按照某种特定的顺序访问树的所有结点。
(1)遍历的分类
● 前序遍历(DLR):访问当前结点,遍历左子树,再遍历右子树。
● 中序遍历(LDR):先遍历左子树,访问当前结点,再遍历右子树。
● 后序遍历(LRD):先遍历左子树,再遍历右子树,访问当前结点。
● 层次遍历。
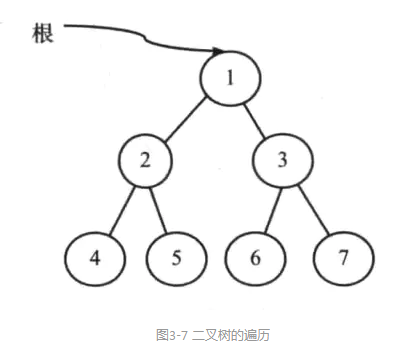
以下图所示的树为例。
①前序遍历
● 基于前序遍历,图3-7所示树的前序遍历结果如下:
前序遍历结果: 1 2 4 5 3 6 7 Process finished with exit code 0
● 递归前序遍历,代码实现如下:
public void PreOrder(BinaryTreeNode root){
if(root!=null){
System.out.print(root.getData());
PreOrder(root.getLeft());
PreOrder(root.getRight());
}
}● 非递归前序遍历,需要采用一个栈来记录当前结点,以便在完成左子树遍历后能返回到右子树进行遍历。首先处理当前结点,在遍历左子树之前,把当前结点保留到栈中,当遍历完左子树之后,该元素出栈,然后找到其右子树进行遍历,直至栈空。代码实现如下:
public void PreOrderNonRecursive(BinaryTreeNode root){
if(root==null){
return;
}
Stack s=new Stack();
while (true){
while (root!=null){
System.out.print(root.getData());
s.push(root);
root=root.getLeft();
}
if(s.isEmpty()){
break;
}
root=(BinaryTreeNode) s.pop();
root=root.getRight();
}
}②中序遍历
● 基于中序遍历,图3-7所示树的中序遍历结果如下:
中序遍历结果: 4 2 5 1 6 3 7 Process finished with exit code 0
● 递归中序遍历,代码实现如下:
public void InOrder(BinaryTreeNode root){
if(root!=null){
InOrder(root.getLeft());
System.out.print(root.getData());
InOrder(root.getRight());
}
}● 非递归中序遍历,与前序遍历的区别是,首先要移动到结点的左子树,完成左子树的遍历后,再将当前结点出栈进行处理。
public void InOrderNonRecursive(BinaryTreeNode root){
if(root==null){
return;
}
Stack s=new Stack();
while (true){
while (root!=null){
s.push(root);
root=root.getLeft();
}
if(s.isEmpty()){
break;
}
root=(BinaryTreeNode)s.pop();
System.out.print(root.getData()+"\n");
root=root.getRight();
}
}③后序遍历
● 基于后序遍历,图3-7所示树的后序遍历结果如下:
后序遍历结果: 4 5 2 6 7 3 1 Process finished with exit code 0
● 递归后序遍历,代码实现如下:
public void PostOrder(BinaryTreeNode root){
if(root!=null){
PostOrder(root.getLeft());
PostOrder(root.getRight());
System.out.print(root.getData());
}
}● 非递归后序遍历,在前序和中序遍历中,当元素出栈后就不需要再访问这个结点了。但是后序遍历中,每个结点需要访问两次。这意味着,在遍历完左子树后,需要访问当前结点,之后遍历完右子树时,还需要访问当前结点。但只有在第二次访问时才处理该结点。
● 解决办法是,当从栈中出栈一个元素时,检查这个元素与栈顶元素的右子结点是否相同。如果相同,则说明已经完成了左右子树的遍历。此时只要再将栈顶元素出栈并输出该结点元素。
public void PostOrderNonRecursive(BinaryTreeNode root){
Stack stack=new Stack();
while (true){
if(root!=null){
//寻找最左叶子结点
stack.push(root);
root=root.getLeft();
}else {
if(stack.isEmpty()){
return;
}else {
//判断当前结点是否有右子节点
if(stack.top().getRight==null){
root=stack.pop();
System.out.print(root.getData()+"\n");
//判断该结点是否为栈顶右子节点
while(root==stack.top().getRight()){
System.out.print(stack.top().getData()+"\n");
root=stack.pop();
if(stack.isEmpty()){
return;
}
}
}
}
if(!stack.isEmpty()){
//遍历结点右子树
root=stack.top().getRight();
}else {
root=null;
}
}
}
}④层次遍历
● 基于层次遍历,图3-7所示树的层次遍历结果如下:
层次遍历结果: 1 2 3 4 5 6 7 Process finished with exit code 0
层次遍历,代码实现如下:
public void LevelOrder(BinaryTreeNode root){
BinaryTreeNode temp;
LLBinaryTreeQueue queue=LLBinaryTreeQueue.creteQueue();
if(root==null){
return;
}
queue.enQueue(root);
while (!queue.isEmpty()){
temp=queue.deQueue();
//处理当前结点
System.out.print(temp.getData()+"\n");
if(temp.getLeft()!=null){
queue.enQueue(temp.getLeft());
}
if(temp.getRight()!=null){
queue.enQueue(temp.getRight());
}
}
}C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程