BFS 全称是 Breadth First Search,中文名是宽度优先搜索,也叫广度优先搜索。是图上最基础、最重要的搜索算法之一。
所谓宽度优先。就是每次都尝试访问同一层的节点。 如果同一层都访问完了,再访问下一层。这样做的结果是,BFS 算法找到的路径是从起点开始的 最短 合法路径。换言之,这条路径所包含的边数最小。
在 BFS 结束时,每个节点都是通过从起点到该点的最短路径访问的。
(1)我们可以用比喻来说明广度优先搜索算法
● 在一片草木枯黄的深秋草原上,在草原的某一处出现了一处野火
● 一开始的时候野火集中于一点之上,在这点野火耗尽当前植被变成灰烬之前点燃了周围的植被
● 比如节点s是初始火种,假设我们手中有一个秒表,每过1秒,我们的大火会向外迈进一步
● 这个过程只能向外,不能向内,因为只能点燃植被,不能把灰烬点燃
● 蓝色的点是即将变为灰烬的点,红色的点是刚被点燃的点,灰色的圆形或圆角矩形是一个前锋面
● 所谓前锋面是火焰向外传播的一个面,frontier
● 之后,每一处的植被都按照同样的模型向外去蔓延, 点燃外层的邻居,前锋面越来越大,最终整个草原燃烧殆尽
● 这个过程是非常自然的,也就是所谓的道法自然,模拟自然的一个过程
● 整个过程,如下图所示
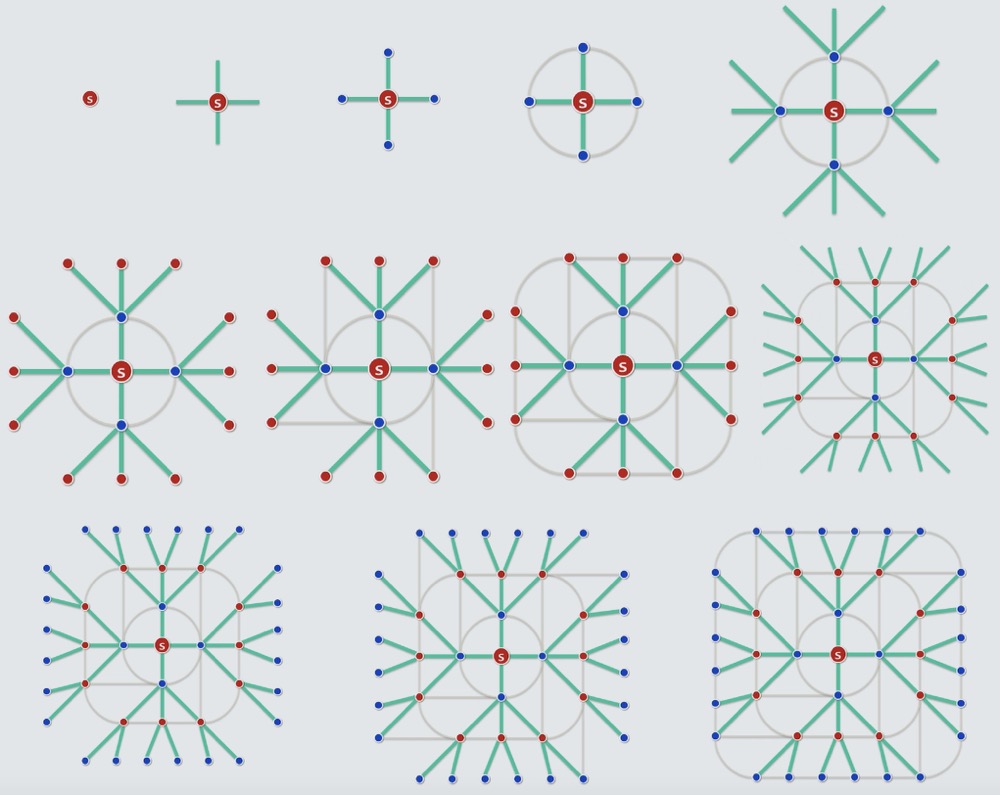
● 任何图结构的模型,只要指定一个节点,比如上图中的s点作为"树根"
● 我们可以把整棵树(图)摊平在某个桌面上,接下来就要开始进行模拟计算
● 如果一个点自己是点燃状态的,那么它接下来就通过一个边去点燃外部的邻居
● 如果邻居是灰烬状态不会被点燃(不会向内部传播),就是这个过程可以点燃整片草原
● 这个方法可以针对s点而言可达的,连通的部分全部访问一遍,这种访问的特点是不重不漏
● 这个方法被称为遍历,也就是traverse或traversal
算法框架实现
template <typename Tv, typename Te>
// v是初始点,clock是读秒器或称为计时器
void Graph<Tv, Te>::BFS(int v, int & clock) {
// 1. 初始化
// 1.1 内部引入一个队列Q, 任何一个点,初始化的时候都是UNDISCOVERED状态,初始的时候v指定为DISCOVERED状态
// 1.2 换种说法:UNDISCOVERED是未燃烧状态,DISCOVERED是燃烧状态
// 1.3 初始点入队
Queue<int> Q; status(v) = DISCOVERED; Q.enqueue(v);
// 2. 处理当前的前锋面上的所有元素
// 2.1 进行循环处理, 循环终止条件是队列变空, 也就是燃烧殆尽
while(!Q.empty()) {
// 反复地,如果不空, FIFO, 并且添加一个时间标签,这里的dTime, d暗示DISCOVERED
// 这时候一个元素独立的占据1s,其实同一个前锋面上的点在自然环境中是同时燃烧的
// 因为我们没法做到, 所以为每一个元素添加一个时间标签,这是一种蹩脚的体现
int v = Q.dequeue(); dTime(v) = ++clock; // 取出队首顶点v
// 考察v的每一邻居u,这个for循环是这个v点的使命,-1<u, 表示u不再是邻居了
for(int u = firstNbr(v); -1 < u; u = nextNbr(v,u)) {
// 根据u的状态,分别处理
if(UNDISCOVERED == status(u)) {
// 若u尚未被发现,则
status(u) = DISCOVERED; // 当前邻居标记成DISCOVERED状态
Q.enqueue(u); // 发现该顶点,将该邻居入队尾,进入前锋面的范围
type(v,u) = TREE; // u之所以会烧起来是被内部的邻居v点燃的, 在将来生成的树中,火传递的方向对应的就是边, 引入树边TREE EDGE
parent(u) = v; // u要把v作为自己的parent
} else {
// 若u已被发现(正在队列中),或者已经能访问完毕(已出队列),将(v,u)归类于跨边
type(v,u) = CROSS;
}
}
// 2.2. 此时,当前顶点访问完毕,也就是v变成了灰烬并且处理完成v所有的邻居
status(v) = VISITED;
}
}● 代码实现可以有很多风格,每种都会有细微的差异,这里的算法是基于c++模板构成的
● 这个算法是模拟自然的过程,最重要的模拟是如何模拟前锋面
● 只要我们模拟出了前锋面(一圈一圈的,一个单位时间,对应一个半径的增长),就模拟出了整个燃烧的过程
● 目前,我们没有什么好的并行机制,将任何时候的前锋面模拟出来,我们需要一个数据结构
● 我们需要把所有前锋面上的所有点都收容进去,但是我们不可能理想的并行的去模拟
● 实际上,前锋面上的每个火源都是各向同性,互不干扰,高效地往外传递,但是我们的计算必须要一个点一个点的处理
● 这些前锋面上的火源表面上看都是相等的,但是我们需要人为的指定一个优先级,比如指定一个点A
● 在处理这个点A的时候,我们要模拟它在燃烧模型中的行为,它的外层邻居如:A1′,A2′,A3′...将被点燃
● 这个时候就有意思了,当它的这些外层邻居都点燃了, 点A就会成为灰烬,就可以被删除了
● 而且理想模型下的点A的同辈:B,C,D…这些在前锋面上的同辈兄弟节点都没有了,都可以被删除了
● 这个时候,就形成了第二个前锋面,但是这个理想型的并发模型,我们无法实现
● 所以,当点A变成灰烬之时,就可以组织第二个前锋面了,我们让点A的外层邻居先进来
● 同样的,点A的同辈兄弟节点按着这个模型依次填充第二个前锋面
● 我们可以知道,第一个前锋面上的所有点A,B,C,D…这些点在构成前锋面的时候是FIFO
● FIFO(Fist In, Fist Out)先进先出,所以,我们需要一个队列Queue来组织每一个前锋面
● 里外前锋面是这样用队列来组织的
①前锋面上的每一个点都排成一个队列,当队头元素A点燃尽的时候, 会被dequeue出队
②之后,被点A点燃的当前外层邻居enqueue入队,之后再以同样的方式处理B,C,D…
● 模拟图如下所示
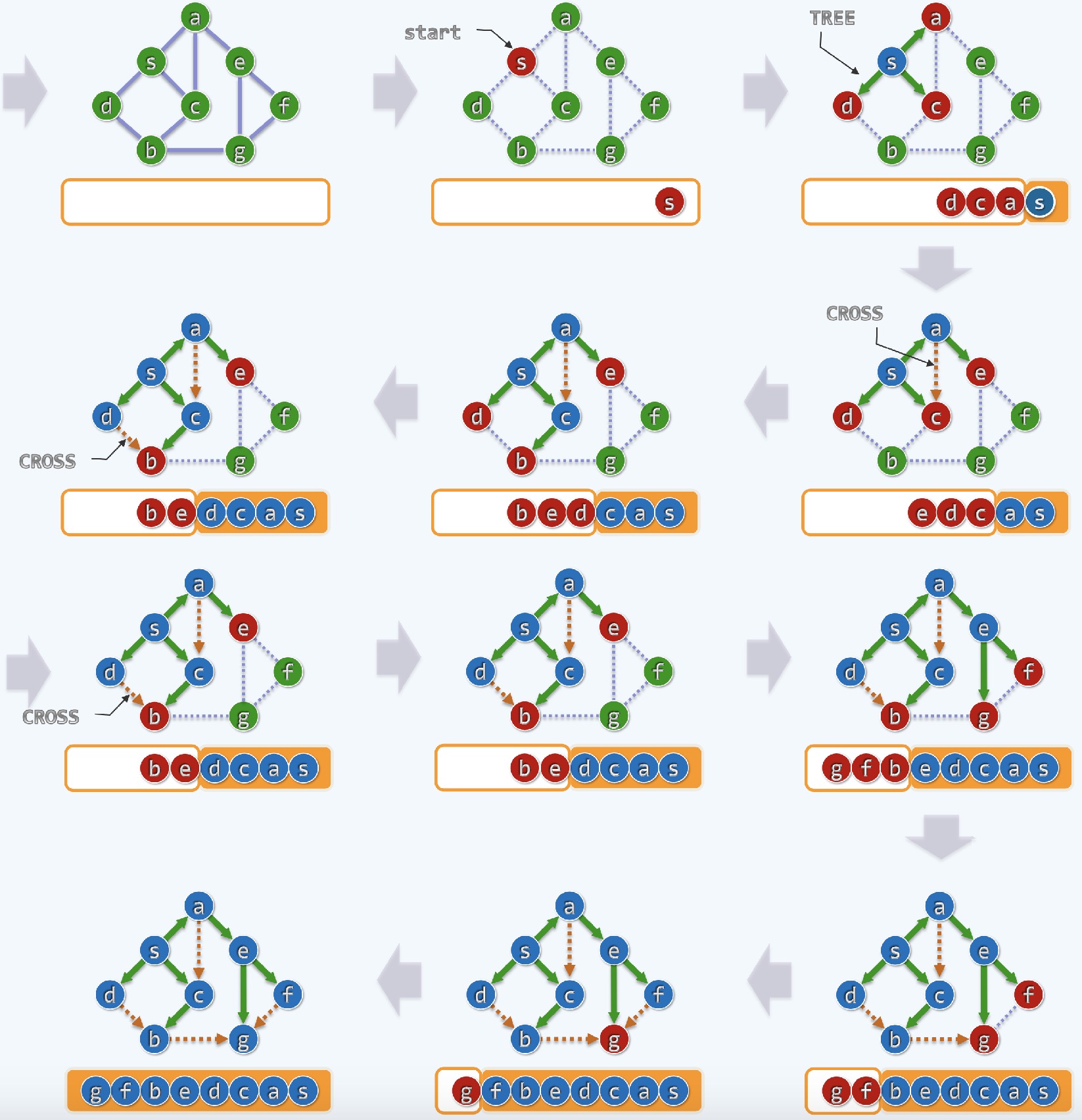
● 上图橙色圆角框代表的是队列,入队的元素是红色的,出队的元素是蓝色的,并且用橙色圆角矩形存储
● 需要注意的是,上述过程中举个例子来说明,当点燃到a的时候,a需要去寻找它的外层邻居,如上图有e和c
● 但是c早已经在s化成灰烬前入队了, 也就是说c是s的外层邻居
● 所以到a的时候,有效的外层邻居只有e, 因为a-c这条路径会构成一条CROSS边
● 绿实线是TREE EDGE,黄虚线是CROSS
①上图中可见,从s-d, s-c, s-a, a-e等绿色的线条都是TREE EDGE
②为什么叫黄色的叫CROSS, 因为它试图连接出一个环出来,这个在树中是禁忌的
● BFS大概就是上述这么一个过程
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程