浅析Garsia-Wachs算法

什么是Garsia-Wachs算法？很多人都觉得这个算法比较陌生，Garsia-Wachs 算法（Garsia-Wachs Algorithm）是计算机用来在线性时间内构建最优二叉查找树和字母霍夫曼码的有效算法。

● 过程：

Garsia-Wachs 算法一般包括三个阶段：

1. 构建一个值位于叶子的二叉树，注意顺序可能错误。

2. 计算树中根到每个叶子的距离。

3. 构建另一个二叉树，叶子的距离相同，但顺序正确。

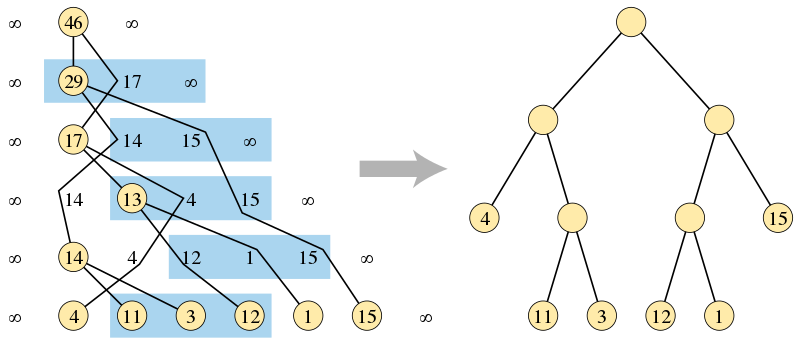
如上图所示，在算法的第一阶段，通过查找合并输入序列的无序三元组构建的二叉树（左侧），和算法输出的正确排序的二叉树，其中叶子高度与另一棵树一样。

如果输入在序列的开始和结束处增加了两个标记值（或任何足够大的有限值），则算法的第一阶段更容易描述。所以在竞赛题解中使用 Garsia-Wachs 算法时，对于一个长度为n的数组，我们一般定义。

第一阶段维护了一个由最初为每个非标志（non-sentinel）输入权重创建的单节点树组成的森林。每棵树都与一个值相关联，其叶子的权重之和为每个非标志输入权重构成一个树节点。为了维护这些值的序列，每端会有两个标记值。初始序列只是叶权重作为输入的顺序。然后重复执行以下步骤，每一步都减少输入序列的长度，直到只有一棵树包含了所有叶子：

（1）在序列中找到前三个连续的权重值x,y,z使得x≤z 。因为序列结尾的标志值大于之前的任意两个有限值，所以总是存在这样的三元组。

（2）从序列中移除x和y，并创建一个新的树节点作为x和y节点的父节点，值为x+y。

（3）在原来x的位置以前大于或等于x+y且距x最近的值的右边重新插入新节点。因为左标志值的存在，所以总是存在这样的位置。

为了有效地实现这一阶段，该算法可以在任何平衡二叉查找树结构中维护当前值序列。这样的结构允许我们在对数时间内移除x和y，并重新插入它们的新父节点。在每一步中，数组中位于偶数索引上直到y值的权重形成了一个递减序列，位于奇数索引位的权重形成另一个递减序列。因此，重新插入x+y的位置可以通过在对数时间内对这两个递减序列使用平衡树执行两次二分查找找到。通过从前一个三元组z值开始的线性顺序搜索，我们可以在总线性时间复杂度内执行对满足x≤z的第一个位置的搜索。

Garsia-Wachs 算法的第三阶段的证明，即存在另一棵具有相同距离的树并且这棵树提供了问题的最优解，是很重要的。但是由于其证明方式有多种且过于复杂，此处略去。在第三阶段为正确的前提下，第二和第三阶段很容易在线性时间内实现。因此，在长度为n的输入序列上，Garsia-Wachs 算法的总时间复杂度为。