什么是后缀数组？

对于后缀数组的概念，很多人都存在疑惑，为什么要学习后缀数组？那么我们就来说说原因，后缀数组是一个比较强大的处理字符串的算法，是有关字符串的基础算法，所以必须掌握。 

学会后缀自动机(SAM)就不用学后缀数组(SA)了？不，虽然SAM看起来更为强大和全面，但是有些SAM解决不了的问题能被SA解决，只掌握SAM是远远不够的。 

……

有什么SAM做不了的例子？ 

比如果求一个串后缀的lcp方面的应用，这是SA可以很方便的用rmq来维护，但是SAM还要求lca，比较麻烦，还有就是字符集比较大的时候SA也有优势。 

在计算机科学里, 后缀数组（suffix array）是一个通过对字符串的所有后缀经过排序后得到的数组。此数据结构被运用于全文索引、数据压缩算法、以及生物信息学。

后缀数组被乌迪·曼伯尔与尤金·迈尔斯于1990年提出，作为对后缀树的一种替代，更简单以及节省空间。它们也被Gaston Gonnet 于1987年独立发现，并命名为“PAT数组”。

后缀数组（Suffix Array）本质上是对一个字符串的所有后缀进行排序，之后会得到两个信息，分别是：

（1）SA[i]，表示排名为 i 的后缀的起始位置。

（2）Rank[i]，表示起始位置为 i 的后缀的排名。

SA数组和Rank 数组是类似反函数的关系，有：SA[Rank[i]]=Rank[SA[i]]=iSA[Rank[i]]=Rank[SA[i]]=i，也就是说如果我求出了其中一个数组，就可以很快知道另一个数组。利用这两个信息，可以处理很多字符串相关的问题。

构造后缀数组——SA

先定义一些变量的含义

Str ：需要处理的字符串(长度为Len) 

Suffix[i] ：Str下标为i ~ Len的连续子串(即后缀) 

Rank[i] : Suffix[i]在所有后缀中的排名 

SA[i] : 满足Suffix[SA[1]] < Suffix[SA[2]] …… < Suffix[SA[Len]],即排名为i的后缀为Suffix[SA[i]] (与Rank是互逆运算) 

好，来形象的理解一下 

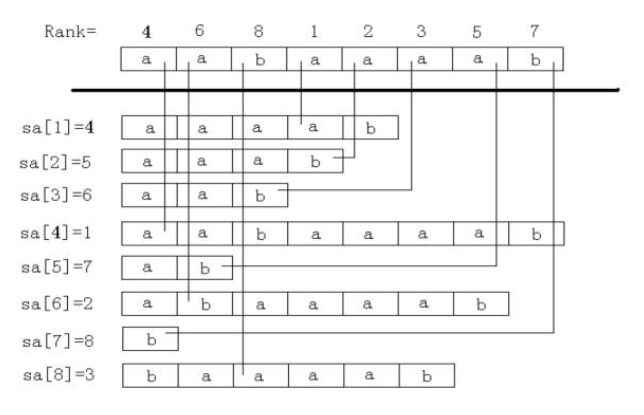
后缀数组指的就是这个SA[i]，有了它，我们就可以实现一些很强大的功能(如不相同子串个数、连续重复子串等)。如何快速的到它，便成为了这个算法的关键。而SA和Rank是互逆的，只要求出任意一个，另一个就可以O(Len)得到。 

现在比较主流的算法有两种，倍增和DC3，在这里，就主要讲一下稍微慢一些，但比较好实现以及理解的倍增算法(虽说慢，但也是O(Len logLen)的。

构造最长公共前缀——Height

同样先是定义一些变量

Heigth[i] : 表示Suffix[SA[i]]和Suffix[SA[i - 1]]的最长公共前缀，也就是排名相邻的两个后缀的最长公共前缀 

H[i] : 等于Height[Rank[i]]，也就是后缀Suffix[i]和它前一名的后缀的最长公共前缀 

而两个排名不相邻的最长公共前缀定义为排名在它们之间的Height的最小值。 

跟上面一样，先形像的理解一下： 

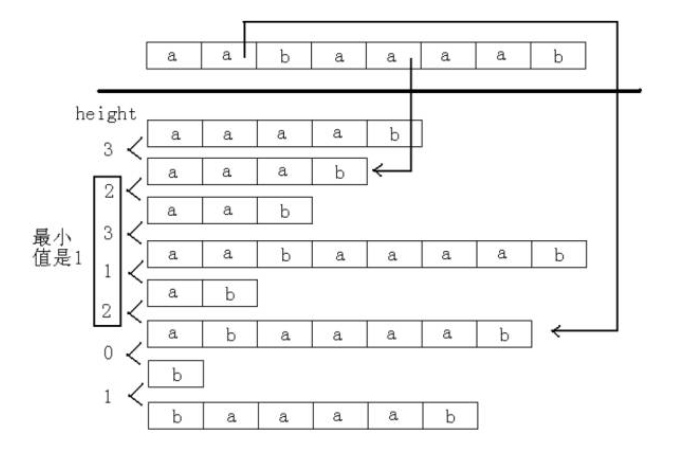
高效地得到Height数组

如果一个一个数按SA中的顺序比较的话复杂度是O(N2)级别的，想要快速的得到Height就需要用到一个关于H数组的性质。 

H[i] ≥ H[i - 1] - 1! 

如果上面这个性质是对的，那我们可以按照H[1]、H[2]……H[Len]的顺序进行计算，那么复杂度就降为O(N)了！ 

让我们尝试一下证明这个性质 : 设Suffix[k]是排在Suffix[i - 1]前一名的后缀，则它们的最长公共前缀是H[i - 1]。都去掉第一个字符，就变成Suffix[k + 1]和Suffix[i]。如果H[i - 1] = 0或1,那么H[i] ≥ 0显然成立。否则，H[i] ≥ H[i - 1] - 1(去掉了原来的第一个,其他前缀一样相等)，所以Suffix[i]和在它前一名的后缀的最长公共前缀至少是H[i - 1] - 1。 

H求出来，那Height就相应的求出来了，这样结合SA，Rank和Height我们就可以做很多关于字符串的题了！