什么是拓扑排序？

拓扑排序主要解决的问题是给一个图的所有节点排序。

一、什么是拓扑排序

在图论中，拓扑排序（Topological Sorting）是一个有向无环图（DAG, Directed Acyclic Graph）的所有顶点的线性序列。且该序列必须满足下面两个条件：

（1）每个顶点出现且只出现一次。

（2）若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

有向无环图（DAG）才有拓扑排序，非DAG图没有拓扑排序一说。

例如，下面这个图：

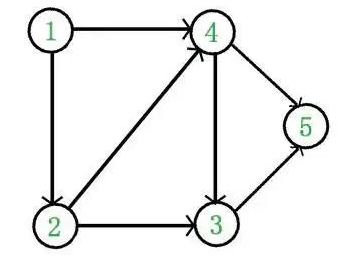
它是一个 DAG 图，那么如何写出它的拓扑排序呢？这里说一种比较常用的方法：

从 DAG 图中选择一个 没有前驱（即入度为0）的顶点并输出。

从图中删除该顶点和所有以它为起点的有向边。

重复 1 和 2 直到当前的 DAG 图为空或当前图中不存在无前驱的顶点为止。后一种情况说明有向图中必然存在环。

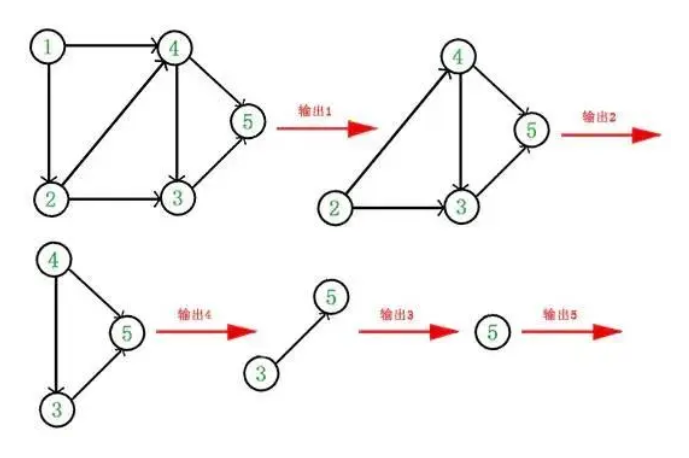
于是，得到拓扑排序后的结果是 { 1, 2, 4, 3, 5 }。

通常，一个有向无环图可以有一个或多个拓扑排序序列。

二、现实案例

看了上面关于拓扑排序的概念如果还觉得十分抽象的话，那么不妨考虑一个非常非常经典的例子 —— 选课。

假设我非常想学习一门《jsp 入门》的课程，但是在修这么课程之前，我们必须要学习一些基础课程，比如《JAVA 语言程序设计》，《HTML 指南》等等。那么这个制定选修课程顺序的过程，实际上就是一个拓扑排序的过程，每门课程相当于有向图中的一个顶点，而连接顶点之间的有向边就是课程学习的先后关系。

只不过这个过程不是那么复杂，从而很自然的在我们的大脑中完成了。将这个过程以算法的形式描述出来的结果，就是拓扑排序。

可以看到，上图中的学习顺序，就是拓扑序列，其不止一个结果。

拓扑排序算法在工程学中十分重要。

节点成环的图，无法被拓扑排序，因为这在工程上本身没有意义，比如 A——>B——>C——>A，那么这个工程永远无法被开始。

三、算法实现

拓扑排序的最优时间复杂度是 O (m+n), 其中 m 和 n 是 DAG 图中节点数和边数。因为拓扑排序至少要对 DAG 图的节点和边进行一次完整的遍历。

拓扑排序的最优空间复杂度是 O (m+n), 其中 m 和 n 是 DAG 图中节点数和边数。我们一般使用邻接表来存储 DAG 图，因此空间复杂度是 O (m+n)。