什么是树上随机游走?我们可以假设给定一棵树,树的某个结点上有一个硬币,在某一时刻硬币会等概率地移动到邻接结点上,问硬币移动到邻接结点上的期望距离。
1. 树上随机游走用到的定义:
● ![]() 所讨论的树
所讨论的树
● ![]() 结点的度数
结点的度数
● ![]() 结点与 v 结点之间的边的边权
结点与 v 结点之间的边的边权
● ![]() 结点的父结点
结点的父结点
● ![]() 结点的子结点集合
结点的子结点集合
● ![]() 结点的兄弟结点集合
结点的兄弟结点集合
2. 向父结点走的期望距离
设![]() 代表 u 结点走到其父结点
代表 u 结点走到其父结点![]() 的期望距离,则有:
的期望距离,则有:
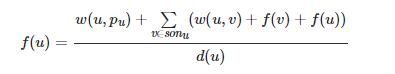
分子中的前半部分代表直接走向了父结点,后半部分代表先走向了子结点再由子结点走回来然后再向父结点走;分母![]() 代表从 u 结点走向其任何邻接点的概率相同。
代表从 u 结点走向其任何邻接点的概率相同。
化简如下:
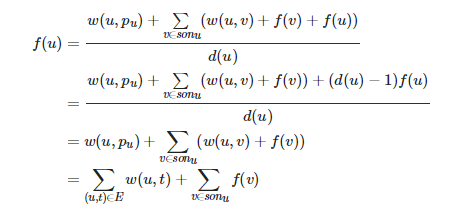
初始状态为![]() 。
。
当树上所有边的边权都为 1 时,上式可化为:
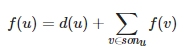
即 u 子树的所有结点的度数和,也即 u 子树大小的两倍-1(每个结点连向其父亲的边都有且只有一条,除 u 与![]() 之间的边只有 1 点度数的贡献外,每条边会产生 2 点度数的贡献)。
之间的边只有 1 点度数的贡献外,每条边会产生 2 点度数的贡献)。
3. 向子结点走的期望距离
设 ![]() 代表
代表![]() 结点走到其子结点 u 的期望距离,则有:
结点走到其子结点 u 的期望距离,则有:
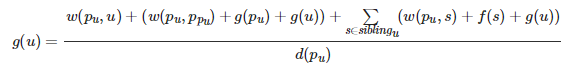
分子中的第一部分代表直接走向了子结点 u,第二部分代表先走向了父结点再由父结点走回来然后再向 u 结点走,第三部分代表先走向 u 结点的兄弟结点再由其走回来然后再向 u 结点走;分母![]() 代表从
代表从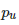 结点走向其任何邻接点的概率相同。
结点走向其任何邻接点的概率相同。
化简如下:
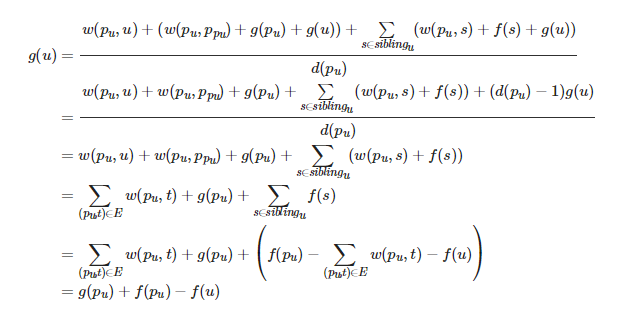
初始状态为![]() 。
。
代码实现(以无权树为例)
vector<int> G[maxn];
void dfs1(int u, int p) {
f[u] = G[u].size();
for (auto v : G[u]) {
if (v == p) continue;
dfs1(v, u);
f[u] += f[v];
}
}
void dfs2(int u, int p) {
if (u != 1) g[u] = g[p] + f[p] - f[u];
for (auto v : G[u]) {
if (v == p) continue;
dfs2(v, u);
}
}
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程