KMP和Z函数

KMP和Z函数，首先要先了解什么是KMP，把KMP了解了，使用Z函数就能更加顺手。很多人初次接触KMP的时候，思路很容易混乱，导致写出来的程序也很混乱。

Knuth-Morris-Pratt字符串查找算法，简称为 “KMP算法”，常用于在一个文本串S内查找一个模式串P的出现位置，这个算法由Donald Knuth、Vaughan Pratt、James H. Morris三人于1977年联合发表，故取这3人的姓氏命名此算法。

KMP可以解决问题类型：

（1）前缀函数：查找子串，每个前缀的出现次数，本质不同子串的个数O(n^2)，字符串压缩：找到t使得s可以被多个t重复出现得到

（2）前缀自动机

举例说明：如果有两个字符串，问：如何快速在一串序列中，找出目标串。

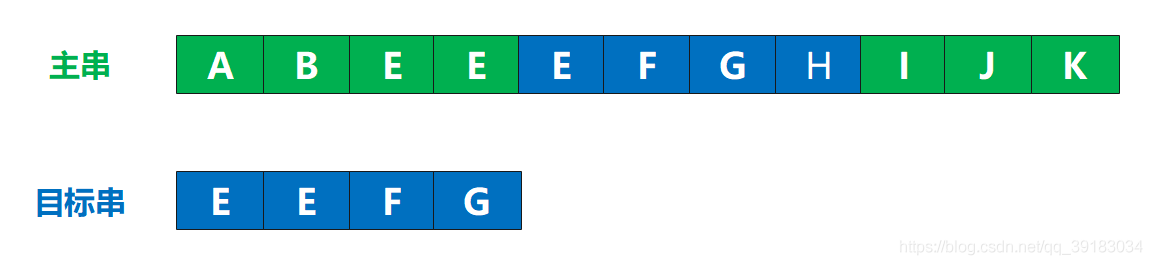
相信很多人拿到题的第一时间就优先想到了暴力破解（用两个指针，开始时分别指向两个串的开头，然后比较，如果相同继续扫描下一个字符，一旦出现不相同，两个指针进行回溯，主串的指针回溯到下一位，目标串的指针回溯至第一位，然后继续按照上述步骤比较）

如图所示

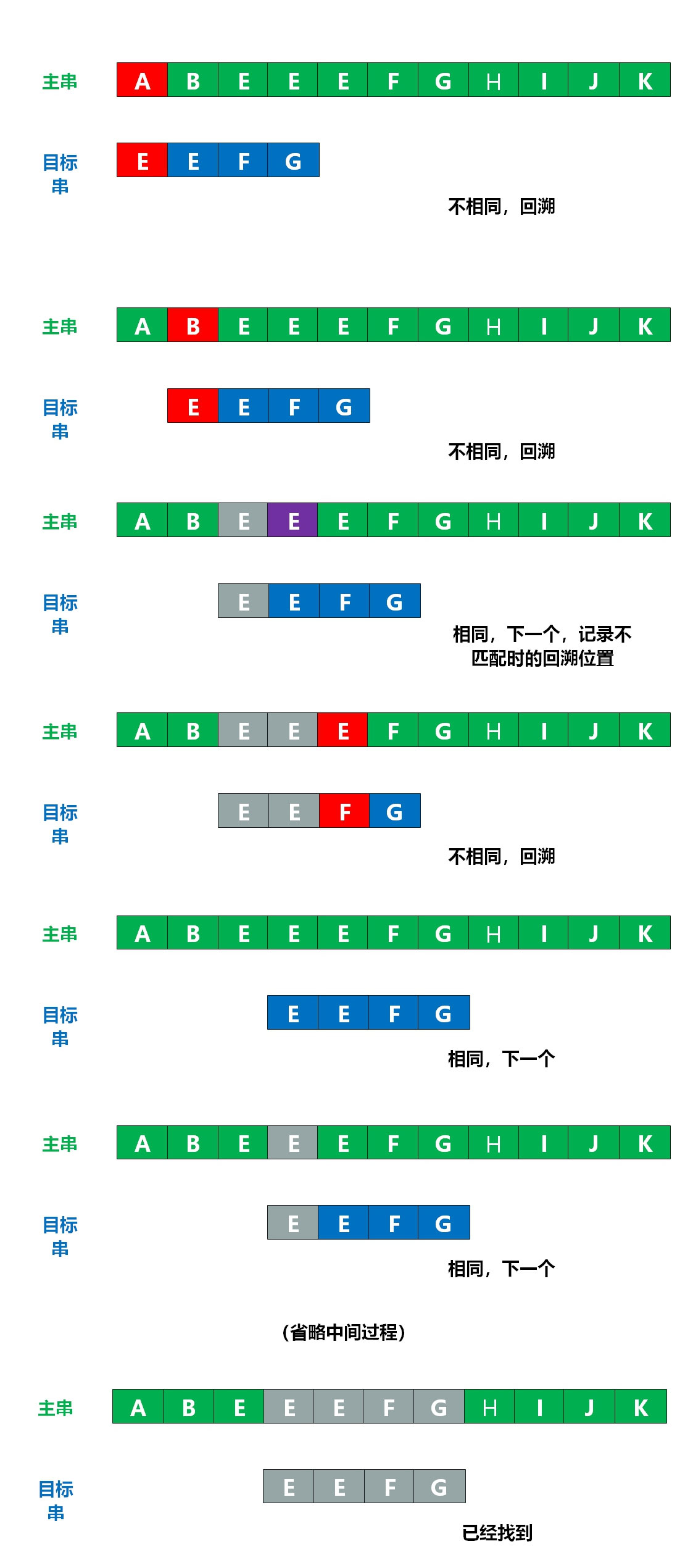
上面的这种暴力匹配是可行的，但是时间复杂度一看就很高，暴力匹配的缺陷所在——回溯太过频繁了。只要出现不匹配就需要回溯到下一位。而KMP算法是为了解决 “如何在主串中快速找到目标串”而孕育出来的算法。

让我们用KMP算法来解答这个问题吧，如图：

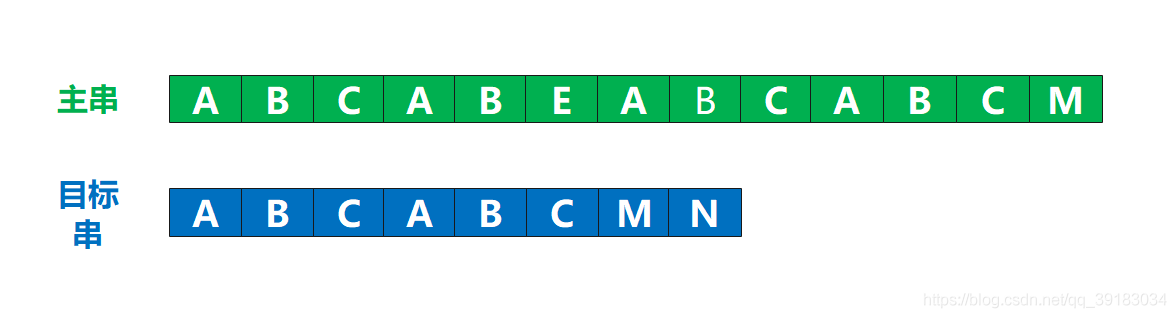
无脑回溯并不合理，比如下面这种情况中，如果让你进行回溯的话，你肯定不会直接回溯到下一位，这是因为你明白直接回溯到下一位会导致连第一位都不会匹配，就更别谈后面了

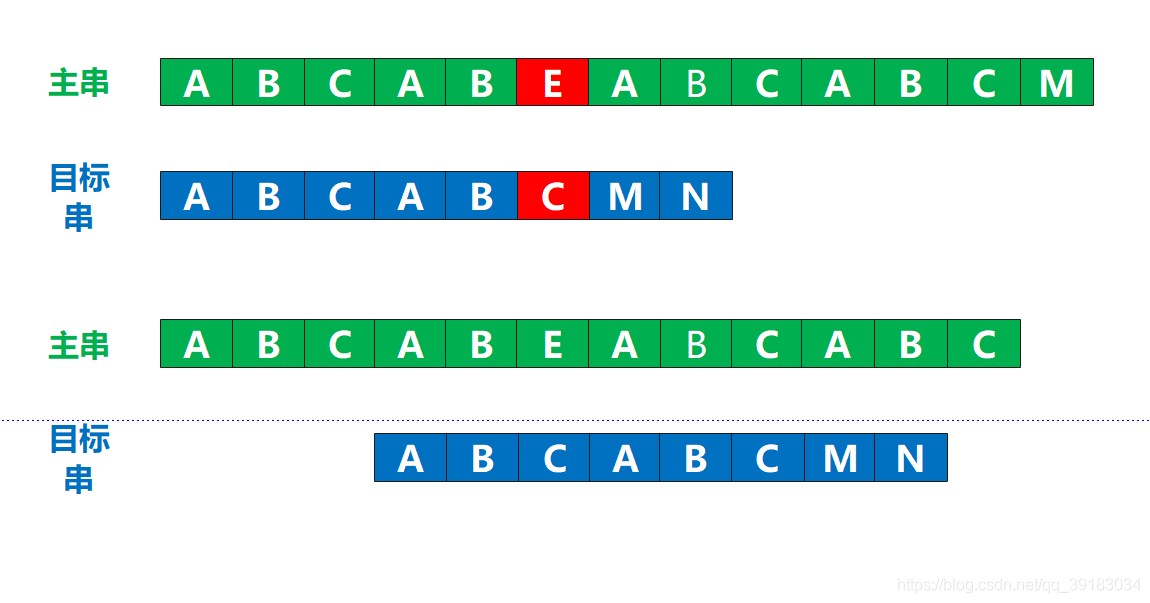
KMP的算法的核心点就在这里：不要回溯到无效的地方，让其回溯到有效的位置

Z函数可以解决问题的类型有：查找子串，本质不同子串的个数O(n^2)，字符串压缩。

定义：前缀函数π(prefix function): π[i]代表子串s[0…i]与其后缀相等的最长真前缀。

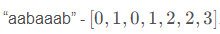
O（n）,在线

vector<int> prefix_function(string s) {
    int n = (int)s.length();
    vector<int> pi(n);
    for (int i = 1; i < n; i++) {
        int j = pi[i-1];
        while (j > 0 && s[i] != s[j])
            j = pi[j-1];
        if (s[i] == s[j])
            j++;
        pi[i] = j;
    }
    return pi;
}

Z函数：z[i]代表串s和其后缀s[i . . . n−1]的LCP，定义z[0]=0

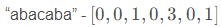
O（n）

vector<int> z_function(string s) {
	int n = (int) s.length();
	vector<int> z(n);
	for (int i = 1, l = 0, r = 0; i < n; ++i) {
		if (i <= r)
			z[i] = min (r - i + 1, z[i - l]);
		while (i + z[i] < n && s[z[i]] == s[i + z[i]])
			++z[i];
		if (i + z[i] - 1 > r)
			l = i, r = i + z[i] - 1;
	}
	return z;
}

关于在KMP与Z函数中，我们还是需要做大量的题，才能更好的运用。