一、定义
边有向,无环。
英文名叫 Directed Acyclic Graph,缩写是 DAG。一个无环的有向图称做有向无环图。
在图论中,如果一个有向图无法从某个顶点出发经过若干条边回到该点,则这个图是一个有向无环图(DAG图)。
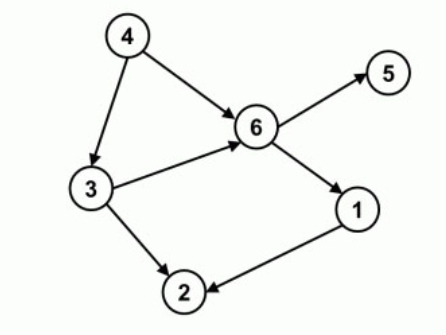
因为有向图中一个点经过两种路线到达另一个点未必形成环,因此有向无环图未必能转化成树,但任何有向树均为有向无环图。
使用有向无环图解题时,要先判断是否是有向无环题。如果任务x必须在任务y之前完成:x→y,而y→z。也就是说一般在涉及优先级限制的问题时,使用有向无环图的方法。
注意与并查集进行区分。
二、有向无环图求解过程
做有向无环图题的时候,一共就三步:
(1)根据题目意思及输入,理清两节点间的指向关系,构建由前指向后的有向无环图。也就是构建一个map,key为当前节点,val数组为当前节点指向的那些节点。
(2)根据有向无环图,统计每个节点出现的次数,因为有的节点已经出现过,但还是可能由其他指向路径的节点再指回来,在输出的时候需要遍历其最后出现的地方,所以要记一下它出现的次数。其中,头节点的次数记为-1,并将头节点保存起来,方便接下来的遍历。
(3)因为有向无环图的输出一般都有要求按大小关系输出(本文按升序输出!),也就是构建一个优先队列来完成节点输出。每遍历一个节点就将其所指向的节点压入队列中,实现了某节点的下一层与当前节点层的其他节点的比较。并将遍历到的节点输出。直到队列中所有节点输出。
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程