栈的定义和特点

数据结构的重要部分，栈，栈是OI中常用的一种线性数据结构，请注意，本文主要讲的是栈这种数据结构，而非程序运行时的系统栈/栈空间，大家一定要弄清晰，别混淆了。

栈的定义和特点

栈（stack）是一个特殊的线性表，是限定仅在一端（通常是表尾）进行插入和删除操作的线性表。又称为后进先出（Last In First Out）的线性表，简称 LIFO 结构。

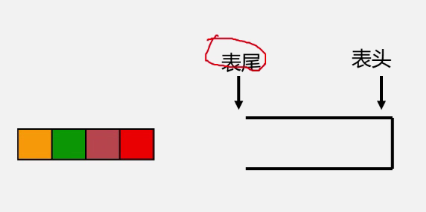
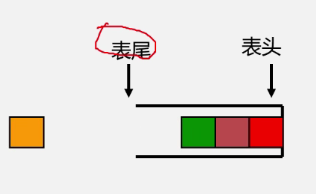
栈的特点：后进先出，先进者后出，就像我们在放盘子，使用的时候先用后放的，后使用先放的。从栈的操作特性上来看，栈是一种“操作受限”的线性表，只允许在一端插入和删除数据。

栈的相关概念：栈是仅在表尾进行插入、删除操作的线性表。

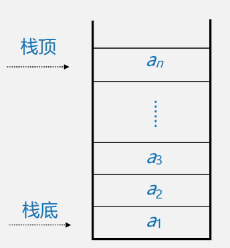
表尾（即an端）称为栈顶 Top；表头（即a1端）称为栈底 Base

例如：栈 s = (a1,a2,a3.....an-1,an)  a1被称为栈底元素，an被称为栈顶元素

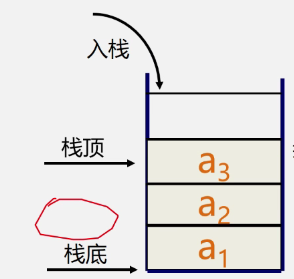
插入元素到栈顶（即表尾）的操作，称为入栈。

从栈顶（即表尾）删除最后一个元素的操作，称为出栈。

栈的示意图：

操作示意图-入栈：

操作示意图-出栈：

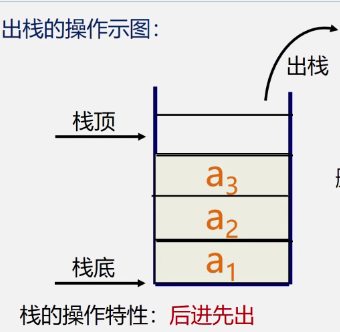
当某个数据集合只涉及在一端插入和删除数据，并且满足先进后出、后进先出的特性，应该首选“栈”这种数据结构。栈的操作包含两个操作：入栈和出栈。

栈既可以用数组实现，也可以用链表来实现。用数组实现的栈叫顺序栈，用链表实现的栈叫链式栈。

对于出栈操作，不会涉及到内存的重新申请和数据的搬移，所以出栈的时间复杂度仍然是O(1)。对于入栈的操作，如果栈中有空闲空间时，入栈的操作时间复杂度是O(1)，当空间不够时，就需要重新申请内存和数据搬移，所以时间复杂度就变成了O(n)。从上述可以看出，入栈的最好情况时间复杂度为O(1)，最坏情况时间复杂度为O(n)。

入栈的时间复杂度如下图所示：

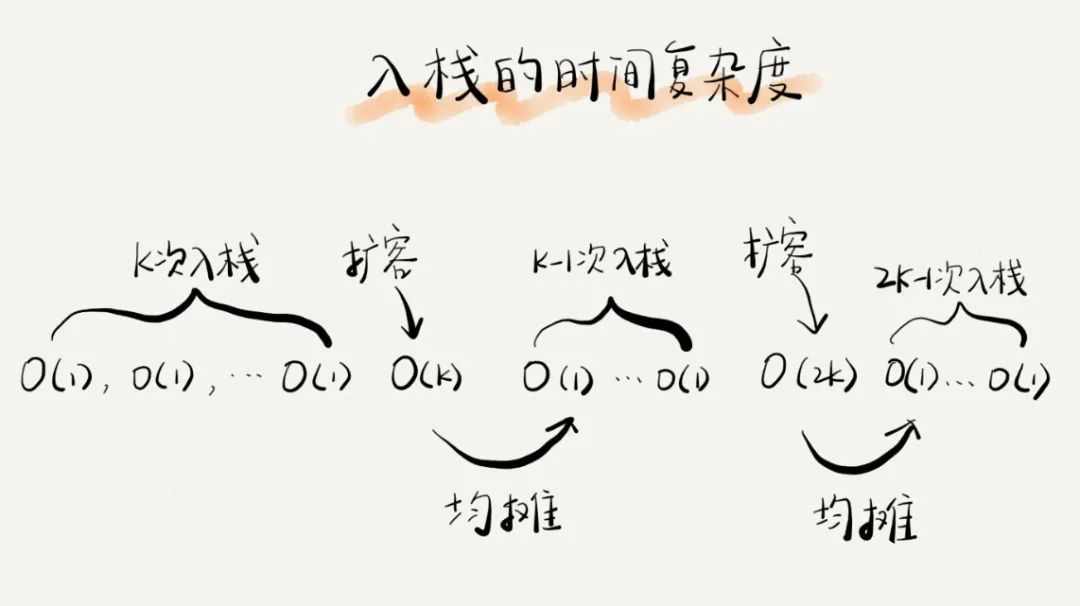
栈在函数调用中的应用

栈作为一个比较基础的数据结构，应用场景还是蛮多的。其中，比较经典的一个应用场景就是函数调用栈。

每进入一个函数，就会将临时变量作为一个栈帧入栈，当被调用函数执行完成，返回之后，将这个函数对应的栈帧出栈。例如下面的这个例子：

int main() {
   int a = 1; 
   int ret = 0;
   int res = 0;
   ret = add(3, 5);
   res = a + ret;
   printf("%d", res);
   reuturn 0;
}

int add(int x, int y) {
   int sum = 0;
   sum = x + y;
   return sum;
}

这个例子调用栈的分析如下图所示：

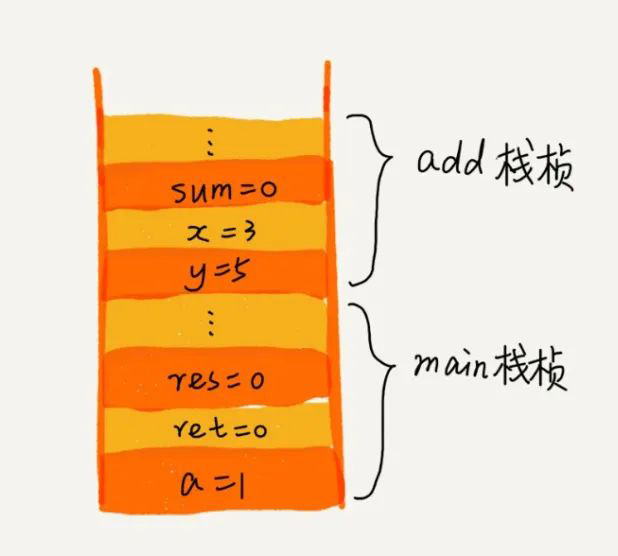
我们平时使用的浏览器大家肯定不陌生，浏览器中的前进和后退其实就是栈的使用，在访问一个网页时可以理解为入栈操作，返回上一个页面可以理解为出栈操作。