树链剖分解决什么问题？

一、什么是树链剖分

什么是树链剖分？它可以把树分成若干条链，从而维护树上的路径信息。本质思想是把树剖成可以用线性结构存储的结构，然后可以数据结构维护。

分为三种：重链剖分、长链剖分、实链剖分。以下以重链剖分为主。

二、树链剖分的思想及能解决的问题

重链剖分可以将树上的任意一条路径划分成不超过O(logn)条连续的链，每条链上的点深度互不相同（即是自底向上的一条链，链上所有点的LCA为链的一个端点）。

重链剖分还能保证划分出的每条链上的节点DFS序连续，因此可以方便地用一些维护序列的数据结构（如线段树）来维护树上路径的信息。

相比之下，树链剖分能解决的很多问题用树上差分也能解决，两者的关系近似于线段树和差分的关系

如：

修改树上两点之间的路径上所有点的值。

查询树上两点之间的路径上节点权值的和/极值/其它（在序列上可以用数据结构维护，便于合并的信息）。

除了配合数据结构来维护树上路径信息，树剖还可以用来O(logn)（且常数较小）地求 LCA。在某些题目中，还可以利用其性质来灵活地运用树剖。

树链剖分的核心就是把一棵树上所有的节点转化为一个序列，当然树的前序遍历中序遍历以及后序遍历都可以实现这一目的，但是我们今天所讲的是另外一种转换方式，如果我们能把树中任意两个节点之间的路径转换为我们所求序列中几段连续的区间我们不就可以用线段树来实现区间修改以及查询了吗？而树链剖分的实现方式可以保证我们把树中任意两点之间的路径转换为不超过logn段序列里面的连续区间，其中n为树的节点个数。

（一）、重链剖分

1. 定义

重子节点：其子节点中子树最大的子结点。如果有多个子树最大的子结点，取其一。如果没有子节点，就无重子节点。

轻子节点：除了重子节点的所有子节点。

重边：从任意节点到重子节点的边。

轻边：从任意节点到轻子节点的边。

重链：若干条首尾衔接的重边，也包括了落单的节点。

如下图 给出了具体的解释

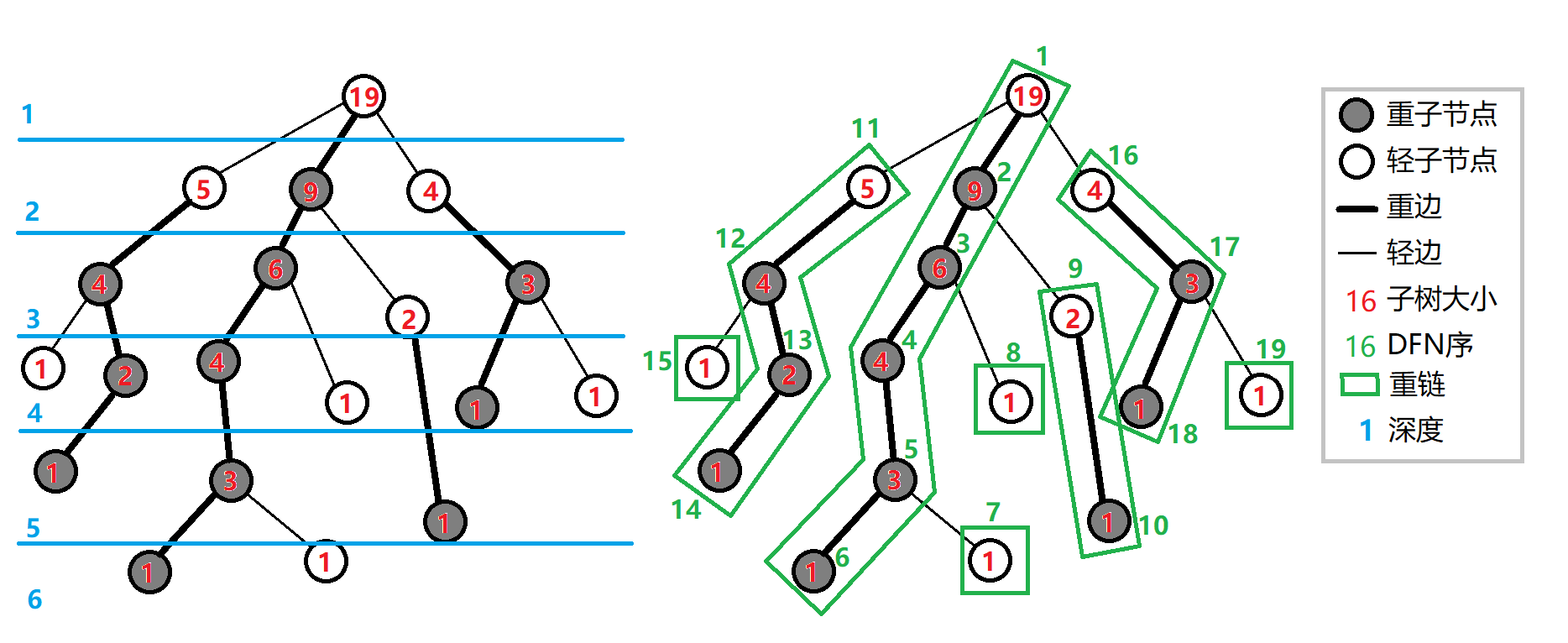
2. 实现

树剖的实现分两个DFS的过程。伪代码如下：

第一个DFS记录每个结点的父节点（father）、深度（deep）、子树大小（size）、重子节点（hson）。

第二个 DFS 记录所在链的链顶（top，应初始化为结点本身）、重边优先遍历时的 DFS 序（dfn）、DFS 序对应的节点编号（rank）。

以下为代码实现。

为了剖出上述重链，我们先给出一些定义：

fa[x]：节点x在树上的父亲。

dep[x]：节点x在树上的深度。

siz[x]：节点x的子树节点个数。

son[x]：节点x的重儿子下标。

top[x]：节点x所在的重链的顶部（深度最小）节点。

dfn[x]：节点x的DFS序，即相当于用数据结构维护时的原始下标。

rnk[x]：dfn反向映射，rnk[dfn[x]]=x。

由两次DFS即可处理出这些信息，第一次处理前四项，后一次处理后四项。

void dfs1(int o) {
  son[o] = -1;
  siz[o] = 1;
  for (int j = h[o]; j; j = nxt[j])
    if (!dep[p[j]]) {
      dep[p[j]] = dep[o] + 1;
      fa[p[j]] = o;
      dfs1(p[j]);
      siz[o] += siz[p[j]];
      if (son[o] == -1 || siz[p[j]] > siz[son[o]]) son[o] = p[j];
    }
}

void dfs2(int o, int t) {
  top[o] = t;
  cnt++;
  dfn[o] = cnt;
  rnk[cnt] = o;
  if (son[o] == -1) return;
  dfs2(son[o], t);  // 优先对重儿子进行 DFS，可以保证同一条重链上的点 DFS 序连续
  for (int j = h[o]; j; j = nxt[j])
    if (p[j] != son[o] && p[j] != fa[o]) dfs2(p[j], p[j]);
}

（二）长链剖分

长链剖分本质上就是另外一种链剖分方式。

重子节点：表示其子节点中子树深度最大的子结点。如果有多个子树最大的子结点，取其一。如果没有子节点，就无重子节点。

轻子节点：表示剩余的子结点。

重边：从这个结点到重子节点的边。

轻边：到其他轻子节点的边。

重链：若干条首尾衔接的重边构成。

把落单的结点也当作重链，那么整棵树就被剖分成若干条重链。

如图（这种剖分方式既可以看成重链剖分也可以看成长链剖分）：

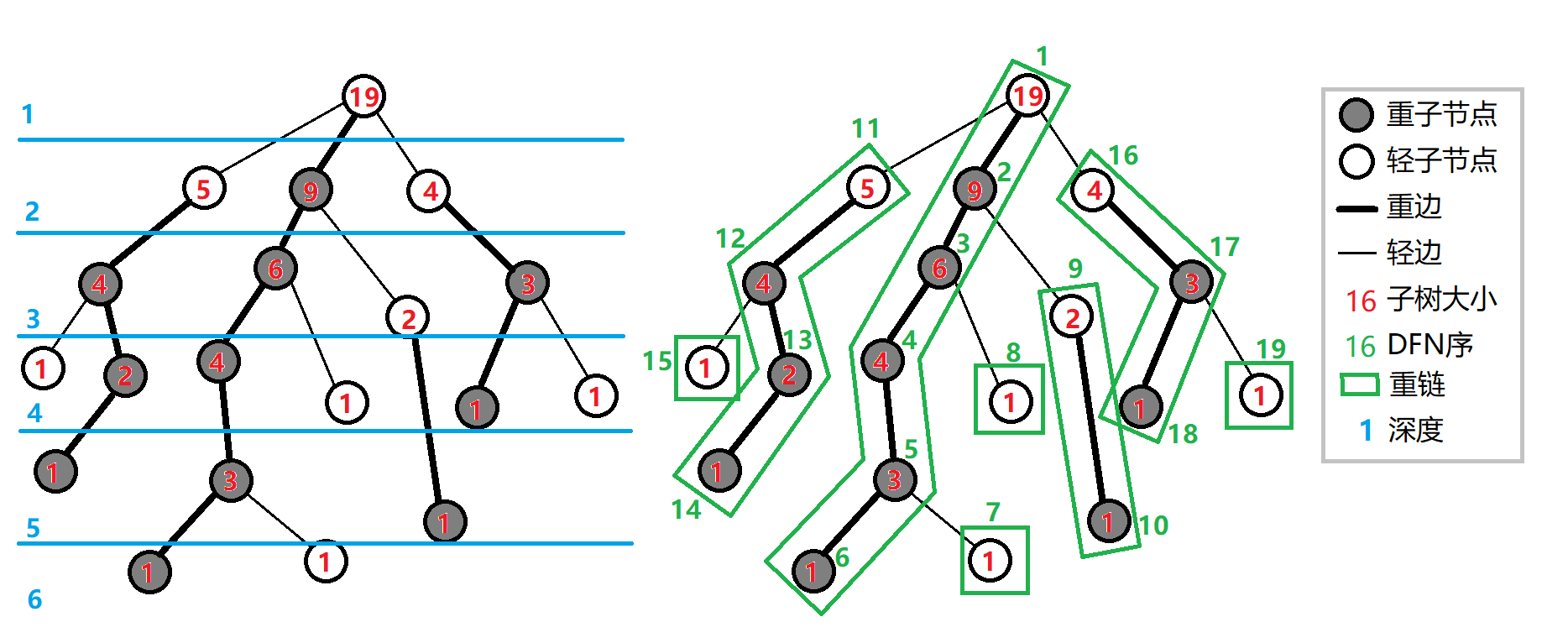
长链剖分实现方式和重链剖分类似，本篇文章就不在详细介绍了，大家可以通过练习来区分和应用。