三角剖分的定义和应用

96966 阅读 0 评论 0 点赞

什么是三角剖分？在几何中，三角剖分是指将平面对象细分为三角形，并且通过扩展将高维几何对象细分为单纯形。对于一个给定的点集，有很多种三角剖分，如：

三角剖分1

OI 中的三角剖分主要指二维几何中的完美三角剖分（二维Delaunay三角剖分，简称DT）。

这个算法本身也不容易，有几个难点，如何高效的找到可疑边和对立点？如果高效的进行点定位（Point Location）操作？即确定插入点落在哪个三角形内部？如何判断点是否在某三个点的外接圆内部？如果能把这几个疑问弄清楚，相信大家用好三角剖分也没有问题了。

三角剖分定义

在数学和计算几何中，对于给定的平面中的离散点集P，其 Delaunay 三角剖分 DT(P) 满足：

（1）空圆性：DT(P) 是唯一的（任意四点不能共圆），在 DT(P) 中，任意三角形的外接圆范围内不会有其它点存在。

（2）最大化最小角：在点集P可能形成的三角剖分中，DT(P) 所形成的三角形的最小角最大。从这个意义上讲，DT(P) 是最接近于规则化的三角剖分。具体的说是在两个相邻的三角形构成凸四边形的对角线，在相互交换后，两个内角的最小角不再增大。

三角剖分定义

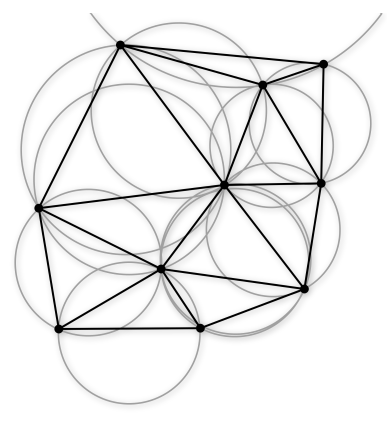
性质

（1）最接近：以最接近的三点形成三角形，且各线段（三角形的边）皆不相交。

（2）唯一性：不论从区域何处开始构建，最终都将得到一致的结果（点集中任意四点不能共圆）。

（3）最优性：任意两个相邻三角形构成的凸四边形的对角线如果可以互换的话，那么两个三角形六个内角中最小角度不会变化。

（4）最规则：如果将三角剖分中的每个三角形的最小角进行升序排列，则 Delaunay 三角剖分的排列得到的数值最大。

（5）区域性：新增、删除、移动某一个顶点只会影响邻近的三角形。

（6）具有凸边形的外壳：三角剖分最外层的边界形成一个凸多边形的外壳。

三角剖分算是一个计算几何里常用的算法，它的构造方案有许多，其中一个算法是 Bowyer-Watson。朴素的 Bowyer-Watson 算法实现复杂度是的，而我使用的这个算法基于的是随机增量方法，期望时间复杂度为。虽然也是暴力，时间复杂度看起来不对，但由于我们是随机的选择插入顺序，超过的情况几乎不存在。