Kirchhoff矩阵树定理可以简称矩阵树定理，可以解决了一张图的生成树个数计数问题。
本篇中的图，无论无向还是有向，都允许重边，但是不允许自环。
一、概况
1. 无向图情况
设G是一个有 n 个顶点的无向图。定义度数矩阵 D(G) 为：
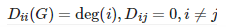
设
为点 i 与点 j 相连的边数，并定义邻接矩阵A为：
定义 Laplace 矩阵（亦称 Kirchhoff 矩阵）L为：
记图G的所有生成树个数为t(G)。
2. 有向图情况
设G是一个有 n 个顶点的有向图。定义出度矩阵
为：
类似地定义入度矩阵
设
为点 i 指向点 j 的有向边数，并定义邻接矩阵A为：
定义出度 Laplace 矩阵
为：
定义入度 Laplace 矩阵
为：
记图G的以 r 为根的所有根向树形图个数为
。所谓根向树形图，是说这张图的基图是一棵树，所有的边全部指向父亲。
记图G的以 r 为根的所有叶向树形图个数为
。所谓叶向树形图，是说这张图的基图是一棵树，所有的边全部指向儿子。
二、定理叙述
矩阵树定理具有多种形式。其中用得较多的是定理 1、定理 3 与定理 4。
定理 1（矩阵树定理，无向图行列式形式） 对于任意的 i，都有
其中记号
表示矩阵L(G)的第
行与第
列构成的子矩阵。也就是说，无向图的 Laplace 矩阵具有这样的性质，它的所有 n-1 阶主子式都相等。
定理 2（矩阵树定理，无向图特征值形式） 设
为L(G)的 n-1 个非零特征值，那么有
定理 3（矩阵树定理，有向图根向形式） 对于任意的 k，都有
因此如果要统计一张图所有的根向树形图，只要枚举所有的根 k 并对
求和即可。
定理 4（矩阵树定理，有向图叶向形式） 对于任意的 k，都有
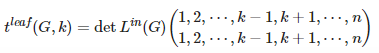
因此如果要统计一张图所有的叶向树形图，只要枚举所有的根 k 并对
求和即可。
BEST 定理
定理 5 (BEST 定理） 设G是有向欧拉图，那么G的不同欧拉回路总数ec(G)是
注意，对欧拉图G的任意两个节点
，都有
，且欧拉图G的所有节点的入度和出度相等。
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程，并配有习题和答疑，点击了解：
一点编程也不会写的：零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码？手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程：算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程