说到分数规划，其实这只是一个用来转换问题模型的一个套路，并没有固定的模板什么的，下面我们看看分数规划的形式和特性。
分数规划(fractional programming) 的一般形式：
对于解空间 S 、连续的实值函数 a(x)，b(x) ，满足 ∀x∈S , b(x)>0，求
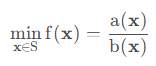
解决分数规划问题的一般方法是分析其对偶问题，但更加实用的方法是对其进行 参数搜索(parametric search)，即对答案进行猜测，再验证该猜测值的最优性，将优化问题转化为判定性问题或其他的优化问题。由于分数规划模型的特殊性，使得能够构造另外一个由猜测值 λ \lambdaλ 作为自变量的相关问题，且该问题的解满足一定的单调性，或其他的可以减小参数搜索范围的性质①，从而逼近答案。
① 比如 Dinkelbach算法，每次直接把上次子问题的解向量代入原问题的表达式，算出下一个迭代式的猜测值。
假设
是最优解，根据定义有
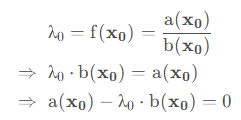
由上面的形式构造一个新函数
这个新函数是一个非分式的规划。先来挖掘函数 g(λ) 本身的性质。
（1）单调性
g(λ) 是一个严格递减函数，即
，
只需要注意到，在
中原有的 x 代入
会得到更小的结果即可。
（2）Dinkelbach定理
若
为原问题的答案，则
1. 必要性
先证明
设
，根据定义有
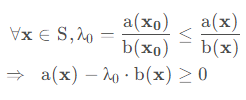
而
恰好取到这个下界 0 ，所以最小值就是 0 ，证毕。
2. 充分性
再证明
反证法。反设存在一个解 λ′= f(x′) 是更优的解，根据定义有
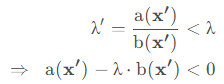
那么，将 x′代入，可以发现 g(λ) 一定是小于零的，与题设矛盾。
（3）二分查找
仍然设
为答案，则
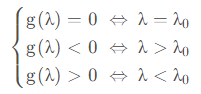
此时便可以进行二分查找了。
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程，并配有习题和答疑，点击了解：
一点编程也不会写的：零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码？手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程：算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程