1. 什么是图
图论(graph theory) 是数学的一个分支,它以 图 为研究的对象。
图论本身是应用数学的一部分,历史上图论曾经被很多数学家各自独立建立过。关于图论的最早文字记载最早出现在欧拉 1736 年的论著中,也就是著名的柯尼斯堡(Konigsberg)问题(七桥问题)。
2. 图的定义
一个图G是一个二元组,即序偶<V,E>,或记作G=<V,E> ,其中V是有限非空集合,称为G的顶点集,V中的元素称为顶点或结点;E称为 G的边的集合,所有的边ei都属于E,都有v中的结点与之对应,称ei为 G的边。
3. 图的基本概念
l 无向图:每条边都是无向边的图。
l 有向图:每条边都是有向边的图。
l 混合图:在一个图中,有些边是有向边,另一些边是无向边,则该图为混合图。
l 有限图:一个图的点集和边集都是有穷集的图。
l 零图:边集为空集的图。
l 平凡图:仅有一个结点而没有边构成的图。
l 关联:若有ei=(u,v) 且ei属于E ,则称u是和v相关联的。
l 孤立点:无边关联的点。
l 自环:若一条边所关联的两个结点重合,则称此边为自环。
l 邻接:关联于同一条边的两个点 和 称为邻接的;关联于同一个点的两条边 和 是邻接的(或相邻的)。
4.两个定理:
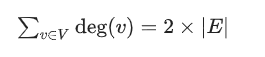
l 推论:在任意图中,度数为奇数的点必然有偶数个。
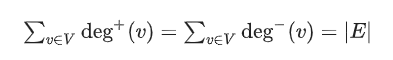
l 推论:即所有点入度之和等于出度之和。
(这个比较好理解,就如同问世界上的上坡多还是下坡多一样,答案是一样多)
由上面的概念可知,树或者是森林,就是一种特殊的图。
5. 最简单的存储——邻接矩阵
邻接矩阵的英文名是 adjacency matrix。它的形式是 bool adj[n][n],这里面n是节点个数,adj[i][j]表示i和j之间是否有边。
如果边有权值,也可以直接用 int adj[n][n] ,直接把边权存进去。
它的优点是可以在O(1)时间内得到一条边是否存在,缺点是需要占用O(n^2)的空间。对于一个稀疏的图(边相对于点数的平方比较少)来说,用邻接矩阵来存储的话,成本偏高。
其代码可以表示为(假设各边长度均为1):
#include<iostream>
using namespace std;
const int maxn=105;
int adj[maxn][maxn]={0}; //定义邻接矩阵
int x,y; //输入两条边
int n,m; //供输入n对边 ,m个顶点 (x,y <= m)
int main(){
cin>>n>>m;
for(int i=0;i<n;i++){
cin>>x>>y;
adj[x-1][y-1]=1;
adj[y-1][x-1]=1;
}
for(int i=0;i<m;i++){
for(int j=0;j<m;j++){
cout<<adj[i][j]<<' ';
}
cout<<endl;
}
return 0;
}C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程