树的遍历之先序遍历二叉树

1. 遍历简介：

树作为非线性数据结构，在我们取出数据时就需要设计遍历，所谓遍历，就是按照一定的规则性，将数据结构中的所有数据全部依次访问，而二叉树本身并不具有天然的全局次序，故为实现遍历，需通过在各节点与其孩子之间约定某种局部次序，间接地定义某种全局次序，这便是我们常规定的先序，中序，后续遍历。

在开始前，请记住下面的这三句话：

先序遍历：根左右

中序遍历：左根右

后序遍历：左右根

2. 先序遍历：

先序遍历就是在访问二叉树的结点的时候采用，先根，再左，再右的方式，对于一个最简单的访问而言如图，先序遍历的访问顺序就是A，B，C

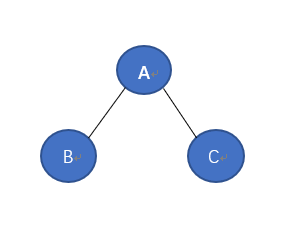
然而实际上的遍历访问并没有那么简单，往往是多个结点相互嵌套构成的二叉树，

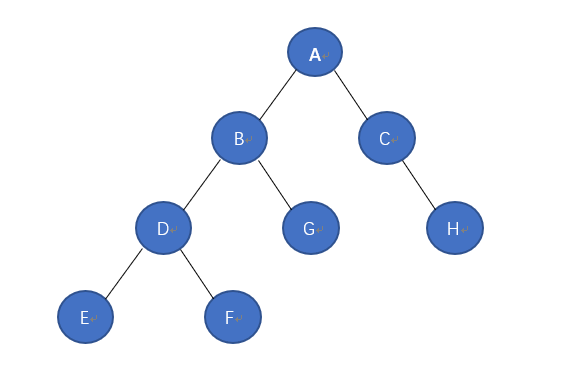
如图所示，在访问遍历一开始的时候，先访问根结点A，次访问左节点B，由于左结点中嵌套了一组结点，因此左节点又作为下一个结点的根结点，因此就继续沿着B访问到了D，同样由于D中包含了一组新的结点，D又作为根节点继续访问，就又访问到了E，由于E没有后面的结点了，作为D为根的左结点E访问结束后，访问到F，这一组访问结束之后再回退访问G……

由此如下的访问规律：这一个二叉树的先序遍历访问顺序就是：ABDEFGCH

3. 代码实现

续上文的代码，实现先序遍历思路非常简单，只需要巧妙的利用“递归”即可。

//树的先序遍历 Preorder traversal
void preorder(Node* node){
    if (node != NULL)
    {
        printf("%d ",node->data);
        inorder(node->left);
        inorder(node->right);
    }
}

4. 扩展：前缀表达式（波兰式）

波兰式又称为前缀表达式，我们日常的运算表达式通常是如下形式，这种成为中缀表达式，也就是运算符在运算数的中间。这种表达式人类人容易识别，并根据其进行计算，但计算机识别这种表达式非常困难。

如图，为常规表达式：(a+b)*c

其二叉树的表现形式为：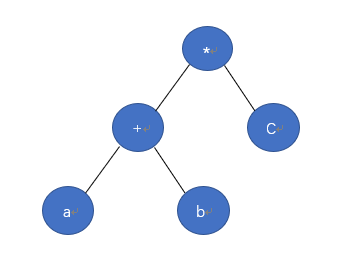

而波兰式的表达方式就是 *+cab ，波兰式的一个特征就是符号迁移，常规的表达式是需要大量的括号表达先后顺序的，而这样的波兰式表达形式不需要，更容易让计算机处理，我们常规的表达式的计算是中序的，而计算机更方便对波兰式这样的方式进行理解，进行这样的转换首先思路要进行转换，在代码中我们实现这样的转换一般可以利用栈，熟练书些这样的转换就需要STL的掌握，这点作为扩展内容自行学习。

5. 相关习题

l  二叉树的遍历习题：https://www.dotcpp.com/oj/problem1734.html

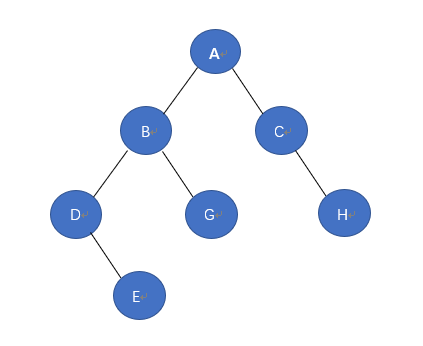
请回答

l  这一颗树的先序遍历是多少？