图的遍历DFS深搜优先搜索及C语言代码实现

1. 图的遍历

在理解DFS算法之前，我们首先需要对什么是遍历进行了解，遍历的概念就是：从某一个点出发（一般是首或尾），依次将数据结构中的每一个数据访问且只访问一遍。

2. DFS简介

DFS（Depth-First-Search，深度优先搜索）算法的具体做法是：从某个点一直往深处走，走到不能往下走之后，就回退到上一步，直到找到解或把所有点走完。

在实现这一个依次的访问顺序时，操作动作存储与数据结构（栈）的思想及其相似，同时也由于栈的性质，我们可以通过递归来简化栈的创建，因此DFS算法的两种做法分别时利用栈或者递归实现。

算法步骤（递归或栈实现）

a)访问指定起始地点。

b)若当前访问顶点的邻接顶点有未被访问的顶点，就任选一个访问。如果没有就回退到最近访问的顶点，直到与起始顶点相通的所有点被遍历完。

c)若途中还有顶点未被访问，则再选一个点作为起始顶点，并重复前面的步骤。

3. 图的DFS

我们直接以案例进行讲解，就本图而言，其访问顺序可以是（不唯一）：1-2-4-5-3

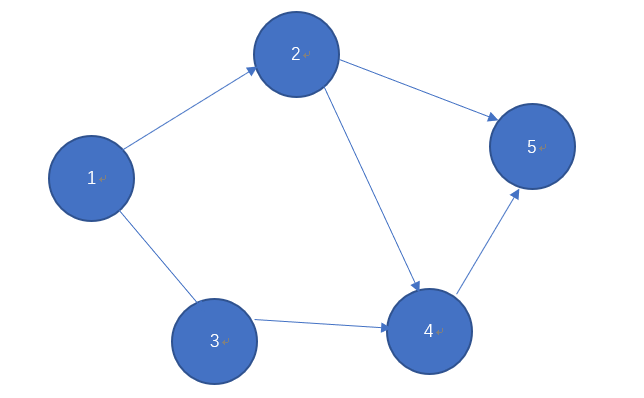
首先从1开始，1结点处可以访问2，3两个结点，那么按照我们自定义的优先顺序线访问2结点，此时，2结点有4，5两个结点访问，依旧按次序访问呢4结点，4结点可以访问5结点，5结点无法继续向下访问故结束访问，并回退4结点，4结点无法没有其他分支且自己已被访问故又退回2结点，2结点的两个分支4，5结点均已被访问，故再退回1结点，此时只有3结点未被访问，访问3结点，最终得到次序：1-2-4-5-3

4.相关代码

DFS算法的相关模板如下：

void dfs()//参数用来表示状态  
{  
    if(到达终点状态)  
    {  
        ...//根据需求添加  
        return;  
    }  
    if(越界或者是不合法状态)  
        return;  
    if(特殊状态)//剪枝，去除一些不需要访问的场景，不一定i俺家
        return ;
    for(扩展方式)  
    {  
        if(扩展方式所达到状态合法)  
        {  
            修改操作;//根据题意来添加  
            标记；  
            dfs（）；  
            (还原标记)；  
            //是否还原标记根据题意  
            //如果加上（还原标记）就是 回溯法  
        }  
 
    }  
}

对于图论而言（代码节选，仅做参考，最主要还请记忆上面的模板那代码）：

//从pos点开始，深度遍历无向图
//pos表示当前结点，G表示图，visited[]数组用来表示该节点是否已经访问
void DFS(int pos,pGraph G,int visited[30]){
    node p;
    printf("%d ",pos);//打印深度遍历的点
    visited[pos]=1;//标记为以访问过
    p=G->vertice[pos].firstarc;//将当前点的第一个指针赋值给p
    //是否存在邻接点
    while(p!=NULL) {
        //判断该邻接点是否被遍历过
        if(visited[p->adjvex]==0){
            DFS(p->adjvex,G,visited);
        }
        p=p->next;//后移一位，为之后是否有邻接点做准备
    }
}

5. 实际应用

在最早期的搜索算法，如HTML的搜索，是基于并利用DFS的，现在诸如一些拓扑图，网络等准确且数据量不大的定位运算等依旧应用非常多的DFS算法，同时DFS算法也是算法竞赛入门级别的标准算法，公司的入职考试算法等。