1. 矩阵扩展算法——简单的算卷积
接着上文,矩阵进行更深入的学习就需要学习更多的处理了,矩阵被运用在很多的领域,这里简单以计算机图形处理的重要概念——卷积,为例进行说明:
卷积。用一个模板去和另一个图片对比,进行卷积运算。目的是使目标与目标之间的差距变得更大。卷积在数字图像处理中最常见的应用为锐化和边缘提取,此外,在人工智能中的图像处理也极为常见,这里的运算介绍不提供繁杂的公式(相信短时间内也看不懂)使用Zero padding,unit strides(零填充,单位滑动)的计算方式进行举例。

(图片来自外国的学术论坛datascience)
对于此类计算,有两个矩阵a和b,矩阵a是原矩阵,b是卷积核,他们的运算过程是,首先对b矩阵进行倒置,如:
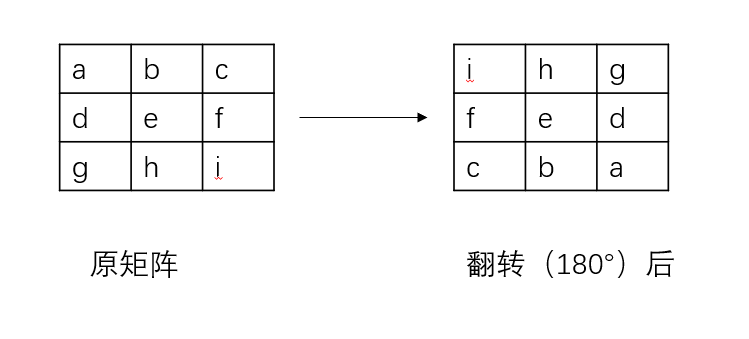
接着,再将待处理矩阵的部分与卷积核进行逐个进行相对应的运算,本例子由于按照边缘’零’处理的方式,因此边缘全部按照0进行运算,如图运算的过程为:0*1+0*2+0*3+0*2+1*1+2*2+0*1+1*2+2*1=9,这样的一个值计算完成后,对每一个值再度进行运算即可。

以卷积核为3*3为例,代码样例为:
#include <iostream>
using namespace std;
const int maxn = 105;
int n,m;
int org[maxn][maxn]={0};
int ker[3][3]={0};
int ans[maxn][maxn]={0};
int main(){
cin>>n>>m;
//待处理的矩阵
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cin>>org[i][j];
}
}
//直接以倒置的方式进行输入
for(int i=2;i>=0;i--){
cin>>ker[i][2]>>ker[i][1]>>ker[i][0];
}
//卷积运算
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
int tmp=0;
for(int a=0;a<3;a++){
for(int b=0;b<3;b++){
tmp += (ker[a][b] * org[i-1+a][j-1+b]);
}
}
ans[i][j]=tmp;
}
}
//结果输出
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
cout<<ans[i][j]<<' ';
}
cout<<endl;
}
return 0;
}2. 杂谈
从前文的代码实现可以看出,矩阵在整个计算机中使用非常广泛,而其实现方式又无不与二维数组这个概念相对应,二维数组是最简单的矩阵表示方式,其便利性可以让我们设计出相当多的矩阵相关的算法,与一维的运算不同,二维的运算无论从理解出发还是计算乃至代码设计出发,都复杂了许多,这就需要充分的数学知识做铺垫,也希望读者能够细细理解代数这一门学科的奥妙。
3.配套习题
更多题目在题库中题库搜索矩阵即可
| 1097 | 蛇行矩阵 |
| 1167 | 矩阵 |
| 1242 | 矩阵转置 |
| 1412 | 矩阵的幂 |
| 1472 | 蓝桥杯基础练习VIP-矩阵乘法 |
| 1550 | 蓝桥杯算法提高VIP-矩阵乘方 |
| 1653 | 蓝桥杯算法训练VIP-矩阵加法 |
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程