java版保证无错题解（蓝桥杯2014年第五届真题-斐波那契）
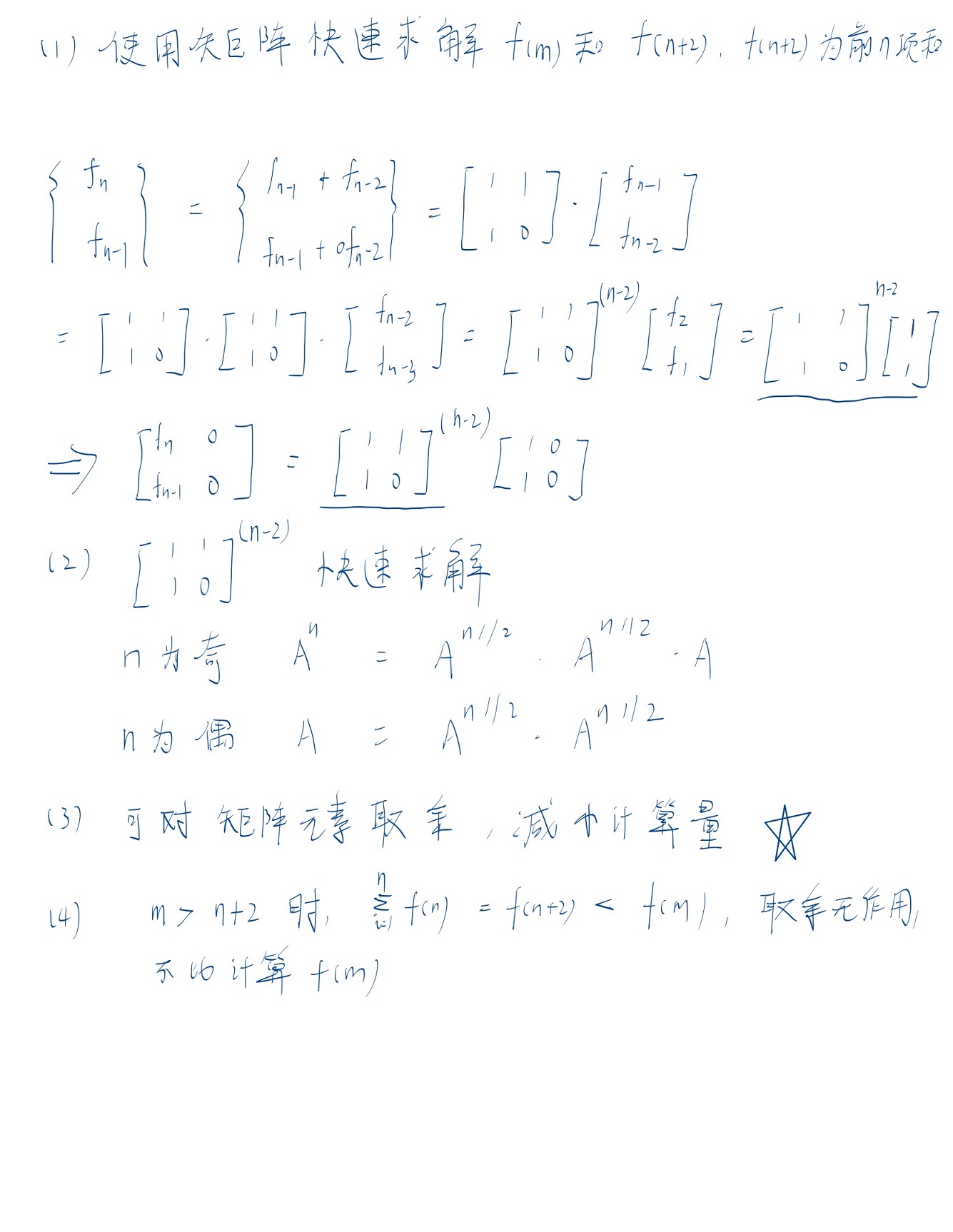摘要：解题思路: 首先请大家自行了解线性代数中的矩阵乘法，矩阵的快速幂，求余数的数学化简公式: 1. (M＋N) mod q=(（M mod q）+（N mod q）) mod q； ……
斐波那契(快速矩阵幂运算)
摘要：斐波那契数列大家都非常熟悉。它的定义是：
f(x) = 1 .... (x=1,2)
f(x) = f(x-1) + f(x-2) .... (x> 2)
对于给定的……
斐波那契数列和，矩阵快速幂
摘要：本题我写的内存超限，不要copy我的代码，但是答案都是正确的，不超出时间，做笔记，以后回来再跟进。有高手也可以给我指出一下怎么提高代码内存优化解题思路:首先先要了解什么是快速幂快速幂的意思是，像2的n……
第五届真题-斐波那契
摘要：#define _CRT_SECURE_NO_WARNINGS#include<stdio.h>int main(){ long long n, m, p; scanf("%lld%lld%lld",……
1444: 蓝桥杯2014年第五届真题-斐波那契
摘要：```cpp
#include
#include
using namespace std;
typedef long long LL;
LL llmul(LL a,LL b,LL mod)
……
矩阵快速幂-python（最后一个运行超时）
摘要：解题思路:注意事项:参考代码:n,m,p = map(int,input().split())# 定义快速幂,k为取模的时候使用def fp(base, power:int, k=float('……
蓝桥杯2014年第五届真题-斐波那契(详细解答）
摘要：在解答本题前，我会先介绍一些待会会用到的知识。1、取模公式：（a+b）%p=(a%p+b%p)%p; (a-b）%p=(a%p-b%p)%p; ……
1444: 蓝桥杯2014年第五届真题-斐波那契(python)
摘要：
### A矩阵分解示例
---C语言---数列求和公式+矩阵快速幂
摘要：解题思路:
1.看题目数据高达10^18次方可以知道暴力没有办法做出来，哪怕是O(N)的时间复杂度也会超时，所以需要想办法优化，求斐波那契数列高项的某些信息，首先想到矩阵快速幂
快速幂算法链接：[……
优质题解
蓝桥杯2014年第五届真题-斐波那契-题解(C++代码)
摘要：######在了解矩阵快速幂之前，我们先要知道快速幂。快速幂顾名思义，就是快速算某个数的多少次幂。其时间复杂度为 O(log₂N)， 与朴素的O(N)相比效率有了极大的提高，它的基本原理是二进制。
……