本题我写的内存超限，不要copy我的代码，但是答案都是正确的，不超出时间，做笔记，以后回来再跟进。
有高手也可以给我指出一下怎么提高代码内存优化
解题思路:
首先先要了解什么是快速幂
快速幂的意思是，像2的n次方，用正常的循环就可以解决，但是当这个n很大的时候，就没有办法使用java中Math.pow来做了。
那怎么用快速幂呢，比如10，我们可以将他转化成2进制1010，就变成了2^3+2^1，时间复杂度变成了log2n，大大优化了。具体操作如下：
1、判断当前数是否为偶数，如果不是偶数，那么就要-1变成偶数，并且先提前将x的1次方给result
2、如果是偶数或者是变成偶数之后，将n/=2（这里用2进制做效率更高），将底数x翻倍，如10^6变成100^3
3、到n=1的时候，已经翻倍成最大了，一次性赋值给result，再次判断为奇数，n变为0，退出循环
参考代码:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 | public class Main { private static int mod = 1000; public static void main(String[] args) { int x = 2; int n = 1000000000; long startTime = System.currentTimeMillis(); int result = fastPower(x,n); System.out.println("结果是："+result); long endTime = System.currentTimeMillis(); System.out.println("运行时间为："+(endTime-startTime)+" ms. "); } private static int fastPower(int x, int n) { int result=1; while(n>0) { if((n&1)==1) { n-=1; result*=x; result%=mod; } n>>=1; x*=x; x%=mod; } return result; }} |
再了解矩阵的快速幂
了解了快速幂之后，矩阵快速幂也是一样的，把当前矩阵带入到上面的x中就可以了，方法很简单。具体操作我在下面讲
斐波那契数列和
当然不可能一个个的数字往上加，时间必然会超限。
f(n+2)=f(n+1)+f(n)
f(n+1)=f(n)+f(n-1)
......
S(n)-S(n-1)=f(n);
S(n)=f(n+2)-f(2);
递推一下，可以得到公式S(n)=f(n-2)-1;
还有一个问题是f(n)怎么求？看下面这张图应该明白了，字有点丑哈
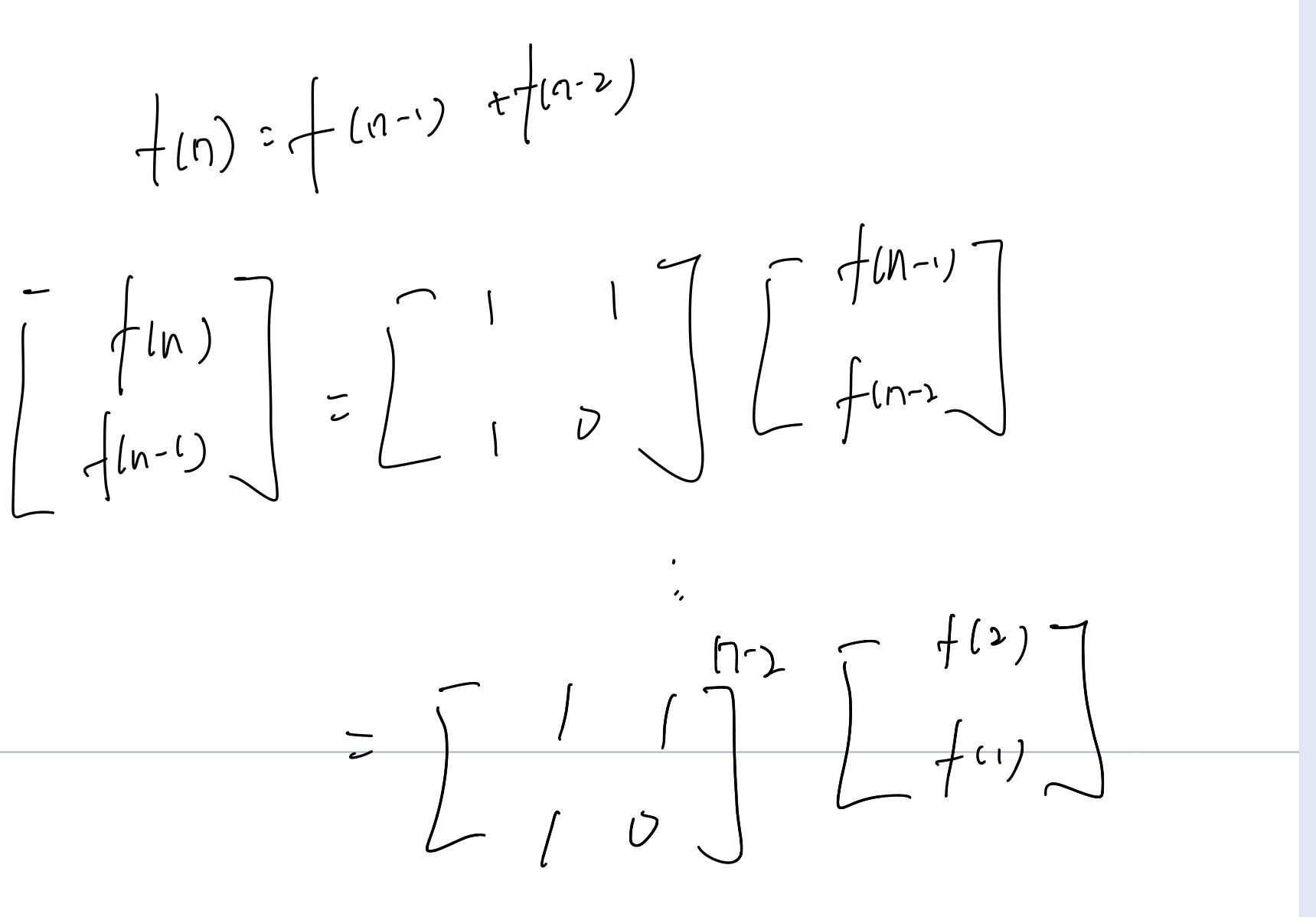
最后就到本题了
我真的巨想吐槽，可恶的java，全是BigInteger，写的太麻烦了，要是有longlong就好了，用BigInteger也用不了位运算，用不了快读快些。哎，估计就出现在这里的内存问题吧
先写一个矩阵相乘的方法，方便矩阵快速幂的运算，这个应该都会，有个问题就是其实矩阵相乘ikj会优化一部分，但是就这样把，水平有限
然后就是矩阵快速幂的运算，如果正常创建一个矩阵默认值会是0，但是BigInteger没有默认值要自己设。然后把数组全部初始化一下。用下上面的快速幂方法，如果是奇数，先把一个当前矩阵给res，如果不是就当前矩阵平方，n/=2
最后调用方法，我可能这里算的有些问题，比如输入的第n个的mutiply（n）会求得n+1个的值，哎无所谓了，程序能跑就行，懒得改了，[0][1]就是求得的值。带入计算即可。
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 | import java.math.BigInteger;import java.util.Scanner;public class Main{ public static void main(String[] args) { Scanner sc=new Scanner(System.in); BigInteger n=sc.nextBigInteger(); BigInteger m=sc.nextBigInteger(); BigInteger p=sc.nextBigInteger(); BigInteger[][] fn=mulpow(n.add(BigInteger.ONE)); BigInteger[][] fm=mulpow(m.subtract(BigInteger.valueOf(1))); BigInteger ans=(fn[0][1].subtract(BigInteger.ONE)).mod(fm[0][1]).mod(p); System.out.println(ans); } //矩阵快速幂算法 public static BigInteger[][] mulpow(BigInteger n){ BigInteger[][] a=new BigInteger[2][2]; a[0][0]=a[0][1]=a[1][0]=BigInteger.ONE; //a为1,1,1,0矩阵 a[1][1]=BigInteger.ZERO; BigInteger[][] res=new BigInteger[2][2]; // 将res设为单元矩阵 相当于整数快速幂中结果的设为1 for (int i = 0; i < 2; i++) { for(int j=0;j0) { if(n.mod(BigInteger.TWO).compareTo(BigInteger.ZERO)!=0) { res=MatrixMutiply(res,a); } a=MatrixMutiply(a,a); n=n.divide(BigInteger.TWO); } return res; } //矩阵乘法 public static BigInteger[][] MatrixMutiply(BigInteger[][] a,BigInteger[][] b){ BigInteger[][] ans=new BigInteger[a.length][b[0].length]; for(int i=0;i<a.length;i++) { for(int j=0;j<b[0].length;j++) { ans[i][j]=BigInteger.valueOf(0); } } for(int i=0;i<a.length;i++) { for(int j=0;j<b[0].length;j++) { for(int k=0;k<b.length;k++) { ans[i][j]=ans[i][j].add(a[i][k].multiply(b[k][j])); } } } return ans; } } |
9.9 分
1 人评分
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程，并配有习题和答疑，点击了解：
一点编程也不会写的：零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码？手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程：算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程
发表评论 取消回复