在解答本题前,我会先介绍一些待会会用到的知识。
1、取模公式:(a+b)%p=(a%p+b%p)%p;
(a-b)%p=(a%p-b%p)%p;
(a*b)%p=(a%p*b%p)%p;
因为C语言的long long最多只能表示19位数,当遇到非常大的数取模时是上面的公式就非常有用。
2、斐波那契数列矩阵求法:

3、快速幂:
求2的1024次幂,用一个for循环可以很快求出,如果是2的10000000000次幂还可以很快就求出接过吗?显然不行。所以,需要用到快速幂的方法。
比如:2^1024 = 4^512 = 16^256 = 256^128 = 65536^64……
按照这种方法设计一个循环,其循环次数会比原先的循环次数减少非常多
(如果读者对快速幂感兴趣可以自行查阅资料,这里只作简单说明)
4、矩阵快速幂:
矩阵快速幂是第二和第三点的结合,通过矩阵的快速幂可以快速地求出第N个斐波那契数。
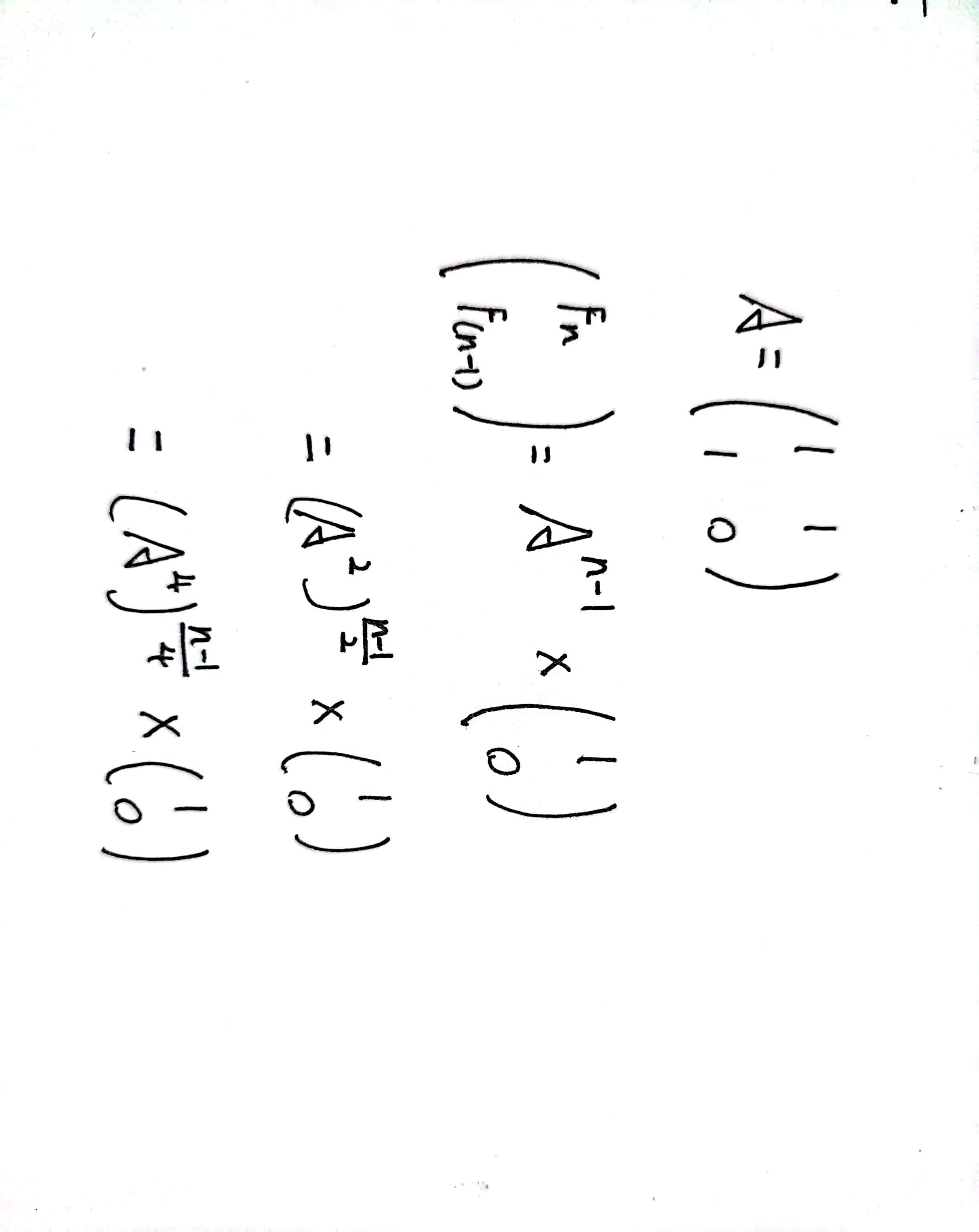
5、斐波那契数列求和:
由F(n)=F(n-1)+F(n-2)可以得到斐波那契数列前n项和 Sn=F(n+2)-1
题目分析:
如果这道题的测试数据很小,那这道题就非常简单。但问题就是这道题的测试数据很大。
因此我们必须考虑两方面:程序执行时间不能超过限制和运算数据不能超过范围(C语言的long long最多只能表示19位数)。程序执行时间可以通过矩阵快速幂 和位运算来减少。而运算数据可以通过大数相乘取模的方法解决(下面会详细分析)。
这道题还要分两种情况讨论:第一种Sn>F(m),Sn需要先对F(m)取模,在对p取模。这里有个小细节,就是Sn和F(m)都不会太大,可以通过硬算得出,因为Sn要 对F(m)取模,而F(m)如果太大是没有办法通过程序计算得出的,所以不用担心F(m)太大。第二种Sn<F(m),Sn无需先F(m)取模,在对p取模,因为Sn对F(m)取模 仍为Sn。
#include <stdio.h>
typedef long long ll; //给long long 定义一个新名字,方便后面使用
long long D[2][2],E[2][2];
void power(ll n); //当SnF(m)时的矩阵快速幂函数
void matrix(ll (*M_1)[2],ll (*M_2)[2]); //当SnF(m)时的矩阵相乘取余 ll (*M_1)[2]是定义了一个可以存储二维数组的指针
int main(){
ll Sn1=0,Sn2=0,fn=0,n,m,p,y;
scanf("%lld %lld %lld",&n, &m, &p);
if(m>n+2){
power1(n+2,p);
Sn1=E[0][1]%p;
y=Sn1-1;
}else if(m1){
if(n&1){ //当n为奇数时 n&1等价于n%2!=0
matrix(A,C); //矩阵A和C相乘
n--;
}
matrix(A,A); //矩阵A和A相乘
n>>=1; //n>>=1 等价于 n/=2 不过位运算可以提高速度
}
matrix(A,C); //矩阵A和C相乘,得出D[0][1]即Sn
void power1(ll n,ll p){
ll A1[2][2]={{1,1},{1,0}},C1[2][2]={{1,0},{0,1}};
while(n>1){
if(n&1){
matrix1(A1,C1,p); //矩阵A1和C1相乘,并对p取余,不然数组内的元素大小会呈现指数型增长,超过范围
n--;
}
matrix1(A1,A1,p); //矩阵A1和A1相乘,并对p取余
n>>=1;
}
matrix1(A1,C1,p); //矩阵A1和C1相乘,并对p取余,得出E[0][1]
}
void matrix(ll (*M_1)[2],ll (*M_2)[2]){ //模拟矩阵M_1和矩阵M_2相乘
int i,j,k,num=0;
ll a[8];
for(i=0;i<2;i++){
for(j=0;j<2;j++){
for(k=0;k<2;k++){
a[num]=M_1[i][j]*M_2[j][k];
num++;
}
}
}
k=0;
for(i=0;i<2;i++){
for(j=0;j<2;j++){
D[i][j]=M_2[i][j]=a[k]+a[k+2];
k++;
}
k+=2;
}
}
void matrix1(ll (*M_3)[2],ll (*M_4)[2],ll p){
int i,j,k,num=0;
ll a[8];
for(i=0;i<2;i++){
for(j=0;j<2;j++){
for(k=0;k<2;k++){
a[num]=POW(M_3[i][j],M_4[j][k],p); //矩阵中大数相乘取余
num++;
}
}
}
k=0;
for(i=0;i<2;i++){
for(j=0;j<2;j++){
E[i][j]=M_4[i][j]=(a[k]%p+a[k+2]%p);
M_4[i][j]=(a[k]%p+a[k+2]%p)%p; //(a+b)%p=(a%p+b%p)%p;
k++;
}
k+=2;
}
}
ll POW(ll a,ll b,ll p) //假设a=456783456789098765 b=231248956706543678 p=612395485768394503
{ //a,b,p都为18位数,a*b%p根本无法计算。这时可以将a*2%p,b/2,其等价于a*b%p
ll sum=0; //如果一次不够就俩次,两次不过就三次,一直持续下去,直到b<=0.由此,可以得到左侧的函数
while(b) //你肯定回想b是奇数怎么办,你可以看看if语句,它就是为了解决这个问题的。
{
if(b&1)
{
sum=sum+a;
sum=sum%p;
}
a=a<<1;
a=a%p;
b=b>>1;;
}
return sum;
}
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
///上面的代码再复制的过程出现了一些问题////////////下面是没问题的//////////////////////////////////////////////////////////////////////////////
#include <stdio.h>
typedef long long ll;
long long D[2][2],E[2][2];
void power(ll n);
void power1(ll n,ll p);
void matrix(ll (*M_1)[2],ll (*M_2)[2]);
ll POW(ll a,ll b,ll p);
void matrix1(ll (*M_3)[2],ll (*M_4)[2],ll p);
int main(){
ll Sn1=0,Sn2=0,fn=0,n,m,p,y;
scanf("%lld %lld %lld",&n, &m, &p);
if(m>n+2){
power1(n+2,p);
Sn1=E[0][1]%p;
y=Sn1-1;
}else if(m<n+2){
power(n+2);
Sn2=D[0][1]-1;
power(m);
fn=D[0][1];
y=(Sn2%fn)%p;
}
printf("%lld",y);
}
void power(ll n){
ll A[2][2]={{1,1},{1,0}},C[2][2]={{1,0},{0,1}},a[8];
while(n>1){
if(n&1){
matrix(A,C);
n--;
}
matrix(A,A);
n >>= 1;
}
matrix(A,C);
}
void power1(ll n,ll p){
ll A1[2][2]={{1,1},{1,0}},C1[2][2]={{1,0},{0,1}};
while(n>1){
if(n&1){
matrix1(A1,C1,p);
n--;
}
matrix1(A1,A1,p);
n >>= 1;
}
matrix1(A1,C1,p);
}
void matrix(ll (*M_1)[2],ll (*M_2)[2]){
int i,j,k,num=0;;
ll a[8];
for(i=0;i<2;i++){
for(j=0;j<2;j++){
for(k=0;k<2;k++){
a[num]=M_1[i][j]*M_2[j][k];
num++;
}
}
}
k=0;
for(i=0;i<2;i++){
for(j=0;j<2;j++){
D[i][j]=M_2[i][j]=a[k]+a[k+2];
k++;
}
k+=2;
}
}
void matrix1(ll (*M_3)[2],ll (*M_4)[2],ll p){
int i,j,k,num=0;;
ll a[8];
for(i=0;i<2;i++){
for(j=0;j<2;j++){
for(k=0;k<2;k++){
a[num]=POW(M_3[i][j],M_4[j][k],p);
num++;
}
}
}
k=0;
for(i=0;i<2;i++){
for(j=0;j<2;j++){
E[i][j]=M_4[i][j]=(a[k]%p+a[k+2]%p);
M_4[i][j]=(a[k]%p+a[k+2]%p)%p;
k++;
}
k+=2;
}
}
ll POW(ll a,ll b,ll p)
{
ll sum=0;
while(b)
{
if(b&1)
{
sum=sum+a;
sum=sum%p;
}
a=a<<1;
a=a%p;
b=b>>1;
}
return sum;
}//75 28 1049 455
//2 3 5 0
//12345 1234567 1000000007 57287399
//7 6 1000 1
//197973570970793793 852595599230933505 836420789208655105 304605587143002279
这是几组测试数据,分别对应n,m,p 和答案
希望这个题解可以帮到你,如果有错误欢迎指正
如有不懂可以私信我,也可以看看其他题解,有个C语言的题解写得很不错
0.0分
3 人评分
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程

发表评论 取消回复