解题思路:
打表理清思路先,把牛家分大牛、三岁牛宝、两岁牛宝、一岁牛宝(虚岁,出生就是一岁啦)
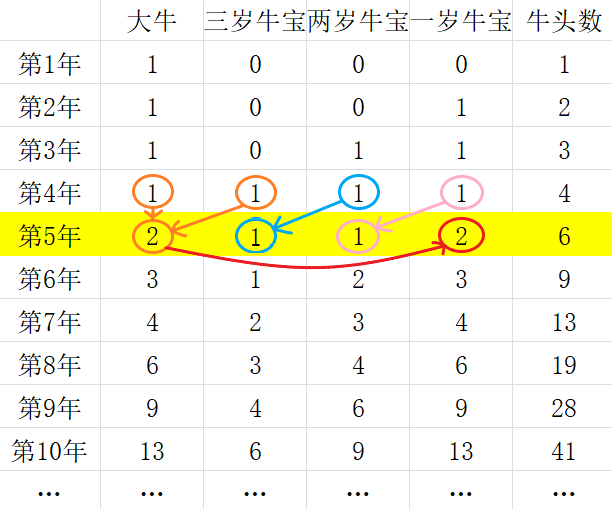
在第5年时,牛宝开始陆续长成大牛,三岁牛宝就变成了大牛
同理,两岁牛宝变三岁牛宝,一岁牛宝变两岁牛宝
而新的一岁牛宝则是去年的大牛跟三岁牛宝的总牛数(三岁牛宝今年长成大牛也开始生小牛宝了)
思路理清后,就要求递推公式了,把4种牛分别用字母标记:
大牛a[]、三岁牛宝b[]、两岁牛宝c[]、一岁牛宝d[]以及牛头数s[]
可以得出第n年的各个公式:
a[n] = a[n-1]+b[n-1]
b[n] = c[n-1]
c[n] = d[n-1]
d[n] = a[n-1]+b[n-1] = a[n]
则总牛数 s[n]=a[n]+b[n]+c[n]+d[n]
= a[n-1]+b[n-1]+c[n-1]+d[n-1]+a[n-1]+b[n-1]
= s[n-1]+a[n-2]+b[n-2]+c[n-2]
= s[n-1]+a[n-3]+b[n-3]+c[n-3]+d[n-3]
= s[n-1]+s[n-3]
根据递推公式可以写出基本的递归函数如下:
int fab(int month) {
if(month < 4) {
return month;
} else {
return fab(month-1)+fab(month-3);
}
}但递归在月份大的时候空间复杂度跟时间复杂度都特别高,故需再用动态规划思路,在递归的过程中不断记录计算过的月份的牛头数,需要的时候可以直接调用
参考代码:
应题目要求使用递归:
#include<iostream>
using namespace std;
long long cow[56] = {0,1,2,3,4}; // 在main函数外定义的数组会全部自动初始化为0
long long fab(int month) {
if(cow[month] == 0) { // 没有算过的月份,数组内存的是0
cow[month] = fab(month-1) + fab(month-3);
return cow[month];
} else {
return cow[month];
}
}
int main () {
int n;
while(scanf("%d", &n) && n) cout << fab(n) << endl;
return 0;
}或者直接用递推公式:
#include<iostream>
using namespace std;
int main () {
int cow[56] = {0,1,2,3,4};
for(int i = 4; i < 55; i ++) cow[i] = cow[i-1] + cow[i-3];
int n;
while(scanf("%d", &n) && n) cout << cow[n] << endl;
return 0;
}0.0分
157 人评分
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程

#include<bits/stdc++.h> using namespace std; int M[20]= {0,31,0,31,30,31,30,31,31,30,31,30,31}; bool isLeapyear(int y) { if((y%4==0&&y%100!=0)||y%400==0) { return true; } return false; } bool check(int y) { int m,d; m = (y%10)*10+((y/10)%10); d = ((y/100)%10)*10+((y/1000)%10); if(m==0||d==0||m>12) { return false; } if(m==2) { if(isLeapyear(y)){ M[2]=29;} else if(!isLeapyear(y)){M[2]=28;} } if(d<=M[m]){return true;} else{return false;} } int ReYear(int y) { return (y%10)*1000+((y/10)%10)*100+((y/100)#include<bits/stdc++.h> using namespace std; int M[20]= {0,31,0,31,30,31,30,31,31,30,31,30,31}; bool isLeapyear(int y) { if((y%4==0&&y%100!=0)||y%400==0) { return true; } return false; } bool check(int y) { int m,d; m = (y%10)*10+((y/10)%10); d = ((y/100)%10)*10+((y/1000)%10); if(m==0||d==0||m>12) { return false; } if(m==2) { if(isLeapyear(y)){ M[2]=29;} else if(!isLeapyear(y)){M[2]=28;} } if(d<=M[m]){return true;} else{return false;} } int ReYear(int y) { return (y%10)*1000+((y/10)%10)*100+((y/100)#include<iostream> #include<vector> using namespace std; int main() { while (true) { int n, num = 1; cin >> n; if (n == 0) { break; } vector<int>age; age.push_back(0); for (int i = 2; i <= n; i++) { int numplus = 0; for (int j = 0; j < num; j++) { age[j] += 1; if (age[j] >= 4) { numplus++; } } num = num + numplus + 1; for (int k = 0; k < (numplus + 1); k++) { age.push_back(0); } } cout << num << endl; } return 0; }为什么不可以#include <iostream> #include <string> using namespace std; #define N 55 int cow[N]; void b(int x); int main() { int n[N]; b(N); int i=0; do { cin >> n[i]; } while (n[i++] != 0); for (int j = 0; j < i-1; j++) { cout << cow[n[j]] << endl; } return 0; } void b(int x) { for (int i = 1; i <= x; i++) { if (i < 4) cow[i] = i; else cow[i] = cow[i - 1] + cow[i - 3]; } }uu们,为啥我这个不行 #include<iostream> using namespace std; long scn[5]={0}; long mcnum=1; void cowreprouce(int year) { if(year<=0) return ; scn[4]+=scn[3]; scn[3]=scn[2]; scn[2]=scn[1]; scn[1]=0; mcnum+=scn[4]; scn[4]=0; scn[1]+=mcnum; if(--year>0) cowreprouce(year); } int main() { int n; long res; cin>>n; if(n==0) return 0; n-=1; cowreprouce(n); res=mcnum+scn[1]+scn[2]+scn[3]+scn[4]; cout<<res; return 0; }为什么这个不行? #include<iostream> using namespace std; int f(int n); int f(int n) { if (n <=4) { return n; } else { return f(n - 1) + 1 + f(n - 4); } } int main() { int n,num[100],i=1; cin >> n; num[0] = n; while (n != 0) { cin >> n; num[i] = n; i++; } cout << endl; for (int j = 0; j < i+1; j++) { if (num[j] != 0) { int sum = f(num[j]); cout << sum << endl; } else { break; } } system("pause"); return 0; }"应题目要求使用递归:"这个代码不对,数组cow应该是={0,1,1,1,1}