动态规划:探讨0-1、完全背包问题(C/C++/Java)

0-1背包(题目:1924):

        给定N个物品,每个物品有一个重量W和一个价值V.你有一个能装M重量的背包.问怎么装使得所装价值最大.每个物品只有一个.

        分析:0-1的意思就是要么拿,那么不拿,物品不可分割,而且每种物品只有一个.

完全背包(题目:2132)

        设有n种物品，每种物品有一个重量及一个价值。但每种物品的数量是无限的，同时有一个背包，最大载重量为M，今从n种物品中选取若干件(同一种物品可以多次选取)，使其重量的和小于等于M，而价值的和为最大。

        分析:完全背包和0-1背包唯一的区别就是每种物品可以拿无数次,而且其他背包的问题都可以转换成0-1背包的思路模式来改进.

思路探讨:

对于任何算法问题我们首先要解决地是把问题存入成数据:

        首先,设w[201](空间要开大点)存放N个物品的各个重量,c[201](空间要开大点)存放N个物品的各个价格,同时设定两个变量n(表示你设定的物品个数),m(表示你设定的物品总质量);

        既然,我们要使用DP(动态规划)来解决问题,就直接设定数组dp[i][j]其中i表示背包中物品的种类数目,j表示背包中的总重量,这样以来我们就可以用个二维数组存放和处理整个问题的所有情况,而且,数组中不同i,j所对应的数组元素存放不同的情况,因为dp[i][j]中存放的就是不同的i(物品)和j(重量)的情况下最大的价值;

        所以最后只需要打印数组中最后一个元素dp[n][m]即为最优数据(所装入的物品价值最大);

        当我们已经将问题用数组和变量确立好关系后,开始探讨整个问题的规律方程,因为动态规划问题归根究底还是要找出问题的状态转移方程式;

很多DP问题都是可以列表来找规律推动态转移方程式,通过假设一组数据来列表确立关系在过程中找规律:

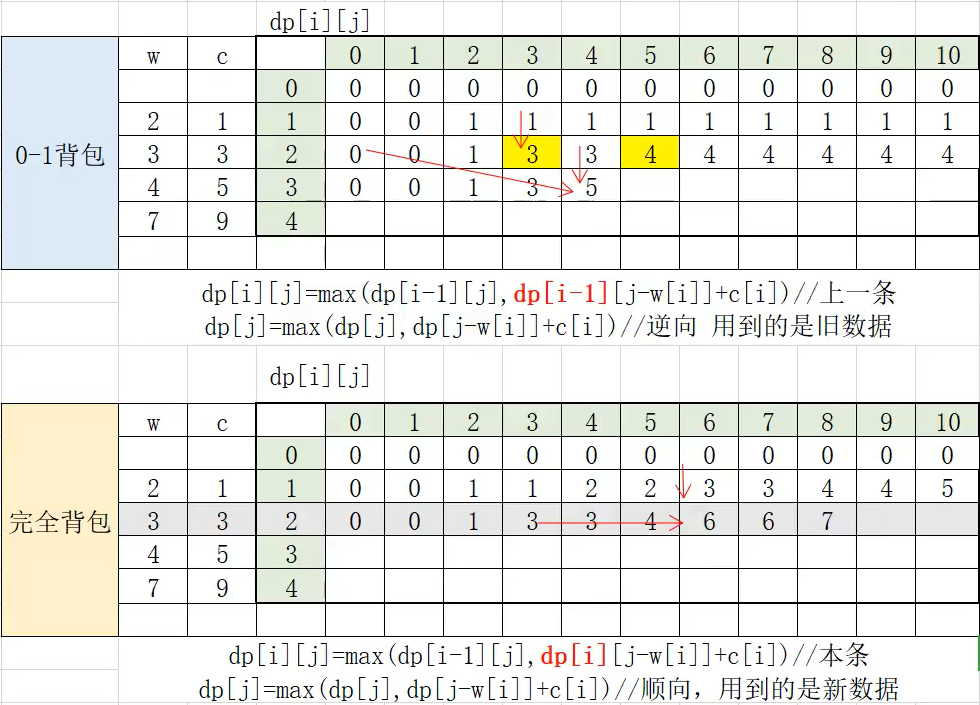
表中我已经给大家明确的列好了

用dp[i][j]表示取前i种物品,使它们总体积不超过j的最优取法取得的价值总和.

0-1背包表中我们用两个for循环从上往下递推:

	for(i = 1;i <= n;i ++)
		for(j = 1;j <= m;j ++)
			if(j<w[i])//当背包重量为j时与物品i的重量做比较 
				dp[i][j] = dp[i-1][j];//背包装不下,只能选择不拿, 
			else
				dp[i][j] = max(dp[i-1][j],dp[i-1][j-w[i]]+c[i]);//max函数库中作用:取两者最大的那一个
				//可能装下,但要让价值最大化,判断装与不装的价值,取最优

但是,我们会发现用二维数组来递推我们需要设很大的空间,所以我们需要空间优化,用一维数组来从上往下一层一层的滚动整个递推过程:

注意:0-1背包我们需要从大往小的递推,防止数组一层执行完到下一层的时候出现数组覆盖的情况

	for(i = 1;i <= n;i ++)
		for(j = m;j >= 1;j --)	//滚动数组要从后往前推,防止数据覆盖 
			if(j >= c[i])		//判断是否能装下 
				dp[j] = max(dp[j],dp[j-w[i]]+c[i]);//把不装的总价值与装下后背包的总价值取最大

完全背包中与0-1背包的思路看上去一样,但却有很大的细微差别:

注意:因为完全背包中物品可以无限被拿,所以我们用朴素的思想就是再用一层循环来执行,同时我们直接用滚动数组(来压缩数组,优化空间)来推断:

	for(i = 1;i <= n;i ++)
	    for(j = 1;j <= m;j ++)
		    for(k = 1;k <= j/w[i];k ++)//我们需要用总重量来除以该物品的重量,看是否还是继续放入,能放入的话在进行判断看哪一种情况价值最大    
			if(j >= w[i])//当背包重量为j时与物品i的重量做比较
				dp[j] = max(dp[j],dp[j-k*w[i]]+k*c[i]);//因为多了一层k循环所以要把判断的物品再乘以k
				//可以装下,不管装入了几个物品,也不管是否相同,但要让价值最大化,判断装与不装的价值,取最优

这种朴素的方法是很好理解,但是本来就两层循环时间复杂度比较高了,又多了一层循环,那我们更需要改进,观察上表中下面的部分来用动态规划的思想来改进:

注意:通过观察上表,可以发现0-1背包问题滚动数组是从上层往下层,而完全背包问题的滚动数组是从顺向而来,所以我们直接根据状态转移规律优化代码,既省时又省空间.

	for(i = 1;i <= n;i ++)
		for(j = w[i];j <= m;j ++)//当背包重量为j时与物品i的重量做比较(顺向)
				dp[j] = max(dp[j],dp[j-w[i]]+c[i]);

通过以上的探究以及代码的实现,我们可以直接用于C/C++/Java来写,代码通用!

我们主要的目的是:

        探究用DP来推导背包问题,通过背包问题来思考动态规划的解题思想,动态规划问题是算法中相对复杂一点的算法思想,需要通过大量题来悟这种思想,加油