位数问题C++题解

解题思路:方法1：排列组合（但需要运用动态规划）

可以列出公式，在n个格子中放x个3（其中x为偶数，包括0）

c(n,x)*9^(n-x)-c(n-1,x)*9^(n-x-1)含义为在n个格子中取x个3，且不考虑第一位的特殊情况为c(n,x)*9^(n-x),而第一位为0的情况为c(n-1,x)*9^(n-x-1),两者相减，就为答案。

              方法2：递推
考虑这种题目，一般来说都是从第一个i-1位推导第i位，且当前位是取偶数还是奇数的。

恍然大悟，可以用f[i][0]表示前i位取偶数个3用几种情况，f[i][1]表示前i位取奇数个3有几种情况。

则状态转移方程可以表示为：

f[i][0]=f[i-1][0]*9+f[i-1][1];   f[i][1]=f[i-1][0]+f[i-1][1]*9;

边界条件：f[1][1]=1;   f[1][0]=9;
注意事项:在所有的2位数字，包含0个3的数有72个，包含2个3的数有1个，共73个
参考代码: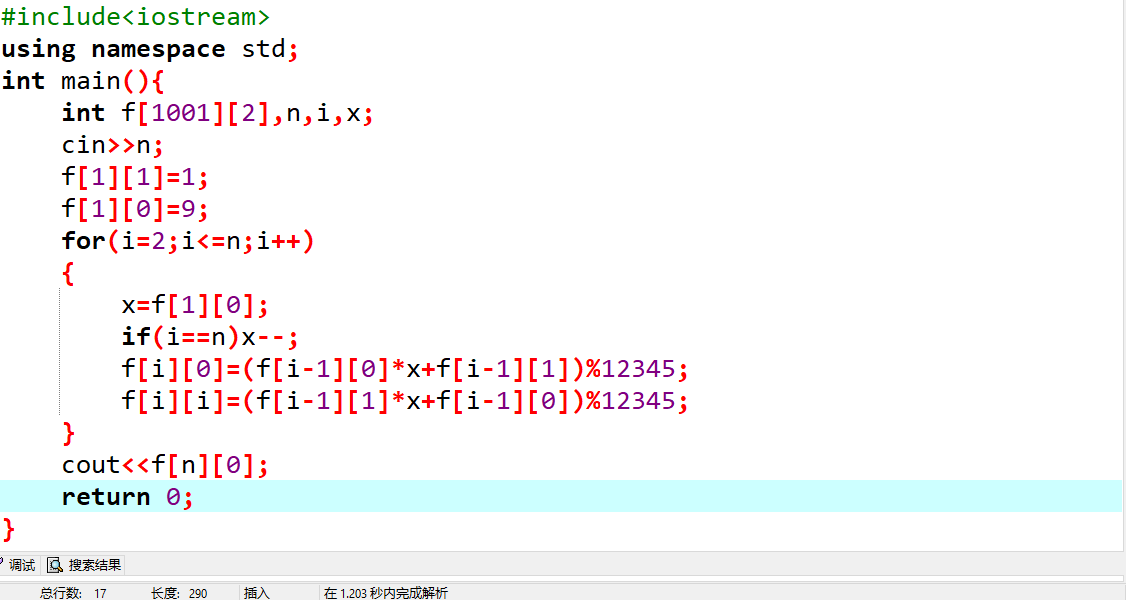代码代码（可复制）：

#include

using namespace std;

int main(){

int f[1001][2],n,i,x;

cin>>n;

f[1][1]=1;

f[1][0]=9;

for(i=2;i<=n;i++)

{

x=f[1][0];

if(i==n)x--;

f[i][0]=(f[i-1][0]*x+f[i-1][1])%12345;

f[i][i]=(f[i-1][1]*x+f[i-1][0])%12345;

}

cout<<f[n][0];

return 0;

} 

第一篇题解，支持一下

（QuQ）