蓝桥杯算法训练1909-拿糖果-JAVA题解（包教包会，带图详细解析动态规划）

解题思路：

    我们先分析题目，有一堆糖果，每次可以拿走x（不大于根号下此时糖果数，且是根号下此时糖果数的质因数）个，拿走x个后，原来的糖果会减少2x，然后重复这个步骤。

  为了更好的理解问题，下面以总共有5个糖果为例，演示过程：

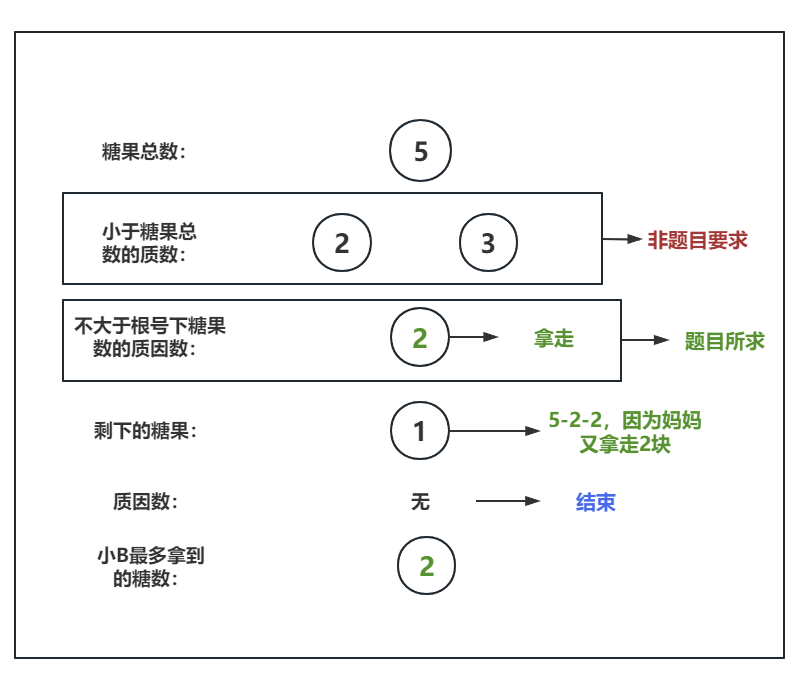
   也就是说，能拿到的最大糖果数是可以往下递推的，因此这是一个动态规划问题。

   设dp[i]为糖果数为i时，小B能拿到的最大糖果数

   动态方程为：dp[i]=max(dp[i],dp[i-2*prime[j]]+prime[j])

                        prime[j]是指第j个不大于根号下此时糖果数，且是根号下此时糖果数的质因数的数

  分析后，需要解决的问题是：

            1、<=（根号n） 的全部质数的数组

            2、获得动态规划结果dp[]

   这里需要注意几点（也是我开始做题漏掉的点）：

           1、我们求的是（根号n）的全部质数的数组，但在循环和判断的时候一直是（根号n），与剩下的糖果

                 数无关

           2、除了是（根号n）的质数，还得是因数

参考代码：

package practice;
import java.util.Scanner;
import java.util.Arrays;
public class NaTangGuo_1909 
{

	public static void main(String[] args)
	{
		Scanner sc=new Scanner(System.in);
		int n=sc.nextInt();
		int dp[]=new int [n+1];
		Arrays.fill(dp, 0);    //填充dp结果数组
		int su[]=new int [n];    //存放<=根号下糖果数的全部质数
		int len=0;   //len表示<=根号下糖果数的质数的个数
		
		for(int i=2;i<=Math.sqrt(n);i++)   //求su[]和len
		{
			boolean flag=true;
				for(int j=2;j<=Math.sqrt(i);j++)
				{
					if(i%j==0)
					{
						flag=false;
						break;
					}
				}			
				if(flag)
				{
					su[len++]=i;
				}		
		}
		
		for(int i=4;i<=n;i++)   //从4开始遍历糖果总数为i时，小B最多可以拿到多少糖果
		{
			for(int j=0;j<len&&(i-2*su[j]>-1)&&j<Math.sqrt(i);j++)   //依次遍历小于等于根号下糖果数的质数数组
			{	
				if((int)Math.sqrt(i)%su[j]==0)   //除了是质数，还得是因数
				{
					dp[i]=Math.max(dp[i],dp[i-2*su[j]]+su[j]);   //动态方程，向下递推
				}		   
			}
		}		
		System.out.print(dp[n]);  //dp[n]表示总糖果数为n时，小B最多能拿到的糖果数	
	}
}