【C语言】数字游戏：从暴力循环到精简代码 - DotcppXF

【解题思路】

        将题目描述的游戏规则转化为数学规律问题，不断优化代码，解决【时间超限】和【数据超范围】两大难点。

【1】常规解法（暴力循环求解）

        ① 直接按题目描述的规则写代码其实很简单，用数组 a[n] 表示每位同学喊出的数字，a[0] 表示栋栋自己的数字；

        ② a[n] 和 a[n-1] 的关系即是：a[n]=a[n-1]+j，j 是从1开始逐渐递增的数，写成代码如下：

s=a[0]=j=1;                              // s表示栋栋自己喊出的数的和，j表示递增数
while(--t)                               // 循环t-1次，t表示栋栋自己说出的数字个数
{
    for(i=1;i<=n;i++)                    // n表示同学数量
    {
        a[i]=(a[i-1]+j)%k;               // 根据题意，数到k-1时便从0开始数
        j++;
    }
    a[0]=a[n];                           // 重新赋值a[0]，准备进入下一次循环
    s+=a[0];                             // s累加栋栋自己喊出的数
}

        ③ 以上方法便能直接解出本题的答案，但面临的第一个问题就是【时间超限】，因为 n,k,t 的取值范围均为2-999999。可以想象一下当n和t都为999999时，上述代码需要进行999998*999999次循环，效率太低了。

【2】等差数列求解（解决时间超限问题）

        ① 其实仔细分析完题目的游戏规则后，同学们喊的数本质上是一个等差数列的和，因为 j 固定的增长量为1；

        ② 假设 f(n) 为第n个同学喊的数，暂不考虑k的情况下，则 f(1) - f(10) 如下表所示：

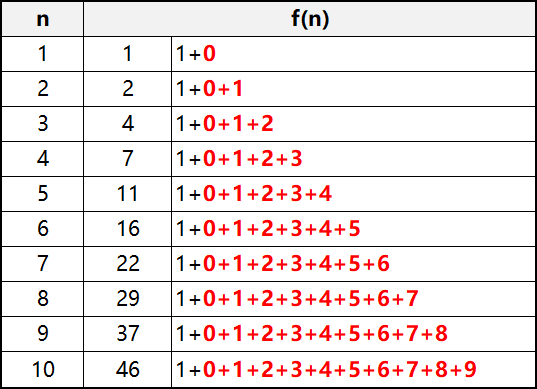
        ③ 根据等差数列的前n项和公式S(n)=a1*n+n*(n-1)/2*d，可以得出f(n)=n*(n-1)/2+1；

        ④ 为了不和题目中的n混淆，我们将第x个同学喊的数f(x)=x*(x-1)/2+1，考虑k的规则后f(x)=(x*(x-1)/2+1)%k；

        ⑤ 但我们并不需要把所有同学喊的数都加起来，我们只需要将栋栋自己喊的数加起来就可以了，假设有n=3，也就是一共只有3个同学，我们需要加上的数如下表黄色的数据部分所示：

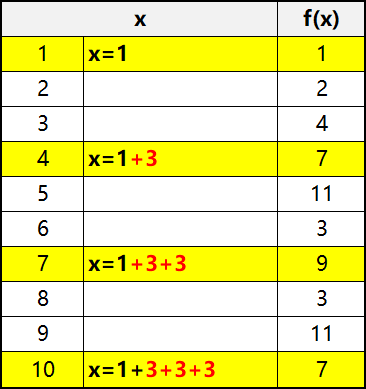
        ⑥ 根据上表能看出我们需要加的项为 f(n*i+1)，n为同学数量，i=0,1,2, ...... t，t为题目中栋栋说出的数字的个数；

        ⑦ 再结合上面 f(x) 的公式，将x=n*i+1，那结果就出来了，f(i)=((n*i+1)*((n*i+1)-1)/2+1)%k，简化一下可得 f(i)=(n*i*(n*i+1)/2+1)%k，写成代码如下：

s=0;                                       // s表示栋栋自己喊出的数的和
for(i=0;i<t;i++)
    s+=(n*i*(n*i+1)/2+1)%k;                // s累加栋栋自己喊出的数

        ⑧ 以上方法只需要一重循环，代码效率提高不少，也无需另开数组，简洁很多。但仍然存在【数据超范围】问题，因为s累加的过程中需要计算n*i*(n*i+1)，i取决于t，当输入的n和t都等于999999时，n*i*(n*i+1)的乘积可达到24位数字，即使是 unsigned long long（最大值18446744073709551615）也无法满足。

【3】取模运算的分配律（解决数据超范围问题）

        ① 取模运算的加法分配律：(a+b)%p=(a%p+b%p)%p；

        ② 取模运算的乘法分配律：(a*b)%p=(a%p*b%p)%p；

        ③ 特别注意取模运算的分配律是没有除法的！！！

        ④ 直接将 (n*i*(n*i+1)/2+1)%k 变更为 ((n*i%k)*((n*i+1)/2%k)+1)%k 是不可行的，因为并不知道n*i能被2整除还是n*i+1能被2整除，因此还需加上一层判断，写成代码如下，这也是解决本题的最终代码了：

s=0;
for(i=0;i<t;i++)
    s+=i*n%2==0?((i*n/2%k)*((i*n+1)%k)+1)%k:((i*n%k)*((i*n+1)/2%k)+1)%k;

【注意事项】

        ① 即使添加了取模运算的分配律变化，数据类型也需要用long long来处理；

        ② s的累加表达式中，取模运算需要判断哪一项能被2整除。

【参考代码】

#include<stdio.h>
   
int main(void)
{
    long long n,k,t,s=0;
    scanf("%lld%lld%lld",&n,&k,&t);
    for(long long i=0;i<t;i++)
        s+=i*n%2==0?((i*n/2%k)*((i*n+1)%k)+1)%k:((i*n%k)*((i*n+1)/2%k)+1)%k;
    printf("%lld",s);
    return 0;
}