二分法总结

定义：

二分查找也称折半查找（Binary Search），它是一种效率较高的查找方法。但是，折半查找要求线性表必须采用顺序存储结构，而且表中元素按关键字有序排列。

编写思路：

通过锚点可以不断改变检索的数组的范围，再在这个范围内通过中值和条件的比较来判断下一步的范围，不断缩小范围，最后到条件符合时跳出循环，输出结果。

注意要点：

在线性表中找的这个结果只能有一个，不确定循环的次数

图解

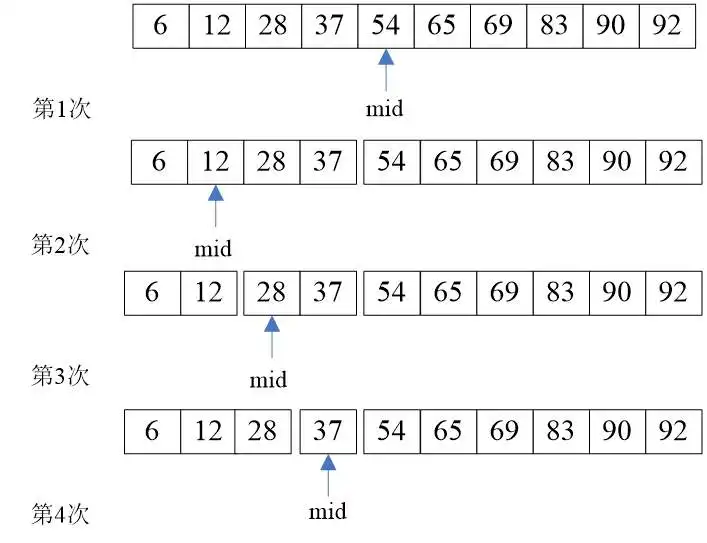
代码注释如下：

/*从小到大输入数组，输出符合条件的数组的下标*/
/*输入格式;第一行输入数组的大小和要查找的数，第二行输入要查找的从小到大排列的数组*/
/*输出格式：要查找的数的下标*/
#include<stdio.h>
int n,x;/*定义的n为数组的大小，定义的x为需要查找的数*/
int a[100];
int find() {
	int left = 0, right = n - 1;
	/*left和right是二分差找的锚点，用于确定查找的范围，这里right设为n-1是因为作为数组的下标*/
	int mid;
	/*mid用于确定中间的那个数组的下标*/
	mid = (left + right)/2 ;
	while(left <= right)
	/*while循环用于不能确定循环次数的情况下，这种二分查找十分适合。
	循环进行的条件是left<=right,当left>right时就意味着查找结束，没有符合条件的自动结束*/
	{
		if (a[mid] > x)
		{
			right = mid - 1;
		}
	/*当所选范围的数组的中值大于条件的值时就意味着所有大于中值的数都不符合条件，
	所以要更改锚点，选择较小的一部分，缩小范围*/
		if (a[mid] < x)
		{
			left = mid + 1;
		}
		/*当所选范围的数组的中值小于条件的值时就意味着所有小于中值的数都不符合条件，
	所以要更改锚点，选择较大的一部分，缩小范围*/
		if (a[mid] == x)
		{
			return mid;
		}
		/*当数组的中值符合条件后，直接返回mid mid就是要查找的数的下标*/
	}
	return -1;
	/*当不符合条件的时候，函数返回-1，用于区分有没有找到的情况*/
}
 
int main()
{
	scanf("%d%d", &n, &x);
	for (int i = 0; i < n; i++)
	{
		scanf("%d", &a[i]);
	}//输入数组
	int rest = find();
	/*用rest存储find函数的返回值，用于接下来的判断*/
	if (rest != -1)
	{
		printf("%d", rest);
	}
	else
	{
		printf("NO");
	}
	return 0;
}

纯代码如下：

#include<stdio.h>
int n,x;
int a[100];
int find() {
	int left = 0, right = n - 1;
	int mid;
	mid = left + right >> 1;
	while(left <= right)
	{
		if (a[mid] > x)
		{
			right = mid - 1;
		}
		if (a[mid] < x)
		{
			left = mid + 1;
		}
		if (a[mid] == x)
		{
			return mid;
		}
	}
	return -1;
}
 
int main()
{
	scanf("%d%d", &n, &x);
	for (int i = 0; i < n; i++)
	{
		scanf("%d", &a[i]);
	}
	int rest = find();
	if (rest != -1)
	{
		printf("%d", rest);
	}
	else
	{
		printf("NO");
	}
	return 0;
}