纯数学递归解法，真的超简单

解题思路:

当我们看到这题时，可能可以想到很多办法，对我而言先想到的是我在概率论学到的知识。

例如7位十进制数 x1 x2 x3 x4 x5 x6 x7

根据题意，第一位数不可能是0，所以x1的选取可以有K-1种。

那么后面的几位都遵循一个原则：

当你的前一位是0时，你只有K-1种选择，当你的前一位不是0，你有K种选择（包括0）。

所以这就成为了一个递归的点。

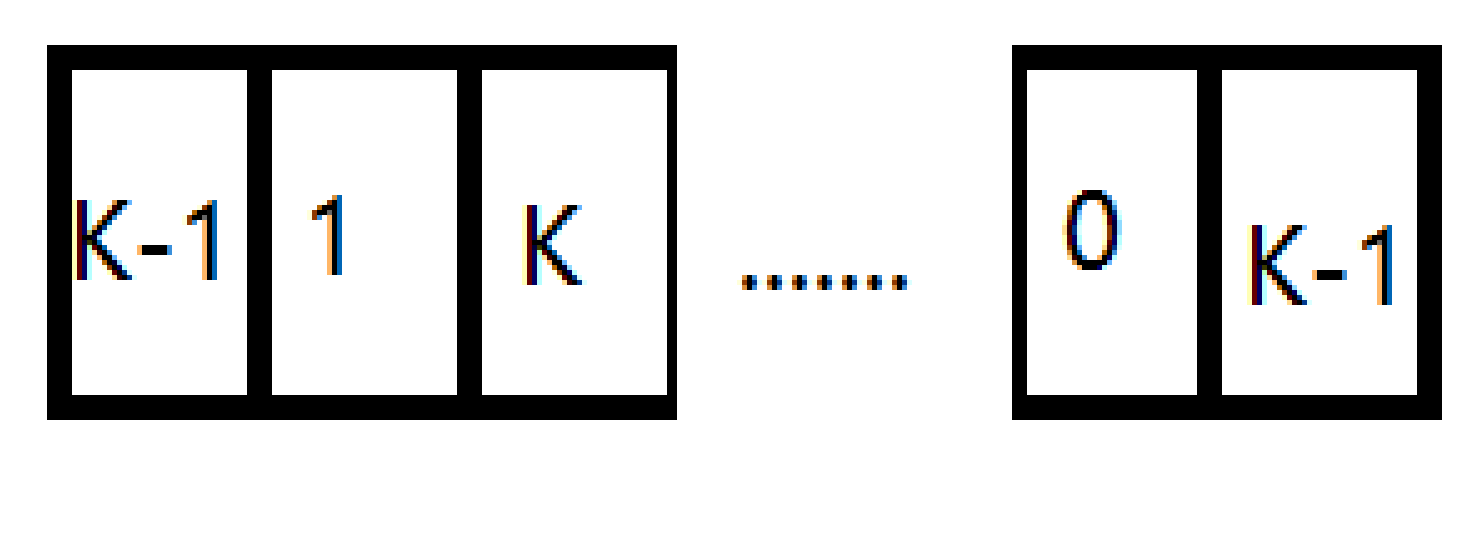
如图，比如第二项不为0，为1，那么下一位就有K种选择。0的下一位就只有K-1种选择。

注意事项:

当某一位为0，那么下一位如果不为0的，那么再下一位就可以取K种。如果下一位为0，那么再下一位就只能取K-1种。

参考代码:

#include<iostream>
using namespace std;

int N,K;
//max是最大位数，now是当前是第几位，pre表示前一个数是否为0，不为0为1
int total(int max,int now,int pre)
{
    if(now==max)
    {
        if(pre==0)
            return K-1;
        else
            return K;
    }
    else
    {
        if(pre==1)
            return total(max,now+1,1)*(K-1)+total(max,now+1,0);
        else if(pre==0)
            return total(max,now+1,1)*(K-1);
    }
}

int main()
{
    cin>>N>>K;
    int res=(K-1)*total(N,2,1);
    cout<<res;
}