分析第二个优质题解

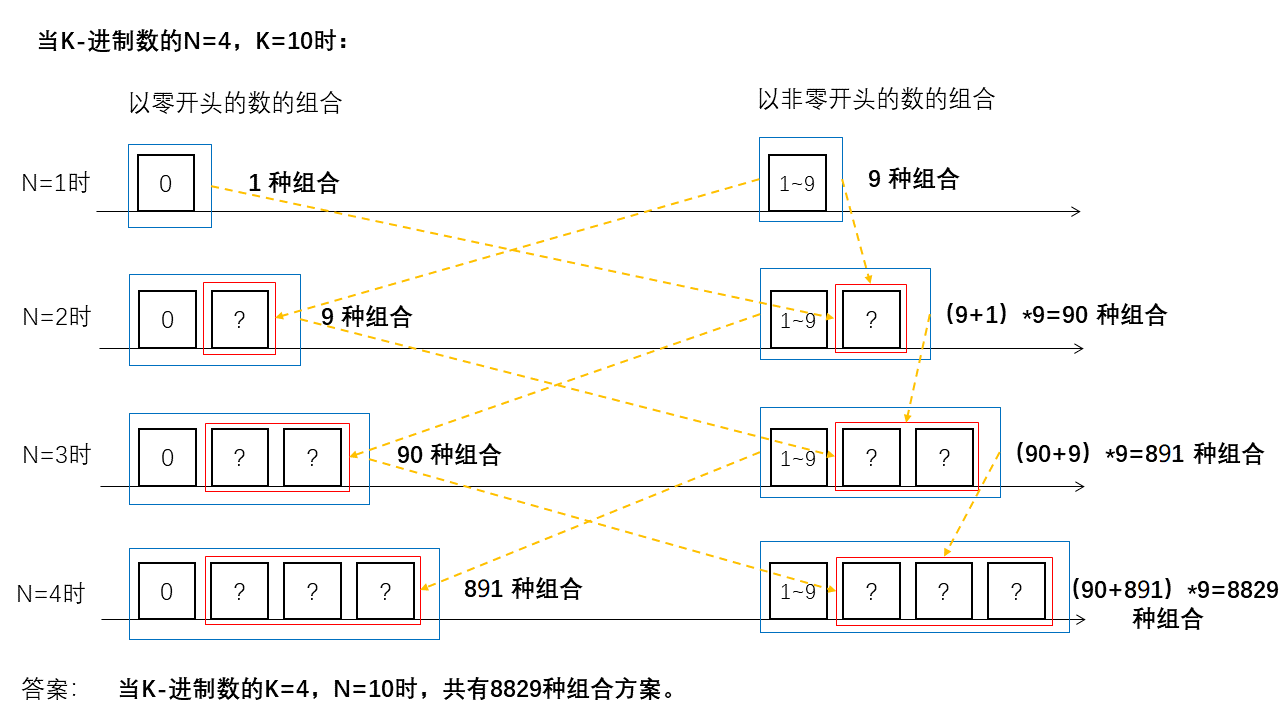
 宏观思路:

    低位数组合的处理较为简便，可以肉眼观察得出；又k位数的组合数量与k-1位数的组合数量恒存在某一特定关系。因此可以通过低位数组合的数量以及这种关系推得任意高位数组合的数量

微观分析：

    对于任意一个N>=2的数字可以视作2部分，最高位 + 其余所有位。对于第二部分，其最高位可以为0也可以不为0，但对于第一部分必然不能为0

因此 N 数量级的组合的第一部分有9种情况，第二部分的组合情况来自N-1数量级的0开头以及N-1数量级的非0开头
注意事项:

参考代码:

#include <iostream>

using namespace std;

int main(){

   int N,K,arr0[20],arr1[20];

   cin>>N>>K;

   arr0[1] = 1, arr1[1] = K-1;

   for(int i=2; i<=N; i++){

       arr0[i] = arr1[i-1];

       arr1[i] = (arr0[i-1] + arr1[i-1])*(K-1);

   }

   cout<<arr1[N];

   return 0;

}