蓝桥杯2013年第四届真题-农场阳光 （C++代码）

解题思路:

本来想是否会有一个好的公式直接求解，但是我太蠢了想不到，所以想了想有没有什么不是数学上提炼公式的方法的而是计算机上能够实现的方法，上课的时候突然灵光一现，可以通过类似微分然后积分的方法，将农场的面积尽量细分成一个一个小格子，然后通过累加没有被圆覆盖的小格子的数量得到没有被阴影覆盖的面积(以下称面积)。

如何判断小格子是否被圆覆盖了呢？也就是这个算法的关键：

一个小格子有四个角(四个点)，就判断这四个点是否被圆覆盖就行了。

情况1：如果四个点到圆心的长度都大于圆的半径，则可以判断这个格子是在圆的外面的，所以在面积+1

情况2：如果四个点到圆心的长度都小于圆的半径，则可以判断这个格子是在圆的里面的，所以面积不变

（其实只通过以上两种情况来计算，只要精度够高，实际上已经可以得到足够近似的答案了）

情况3：如果正好圆的圆弧穿过这个小格子，那么就要判断，小格子被圆覆盖了多少的面积上去，我是这样判断的——依旧是判断四个点到圆心的距离，肯定会有一些点在圆里面，有一些点在圆的外面，我就定一个规定，只有一个点被圆覆盖时，就判断这个小格子是有效的，可以当作一个面积被累加，如果有两个点以上被覆盖，就不能当作一个面积被累加

不断的从第一个小格子累加到最后一个小格子，最后得出答案。

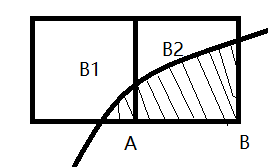
如图中，格子B1的A点被圆覆盖掉，可是他的覆盖的面积不太多，所以视他是一个面积

格子B2中，A点和B点都被圆覆盖掉，可是覆盖的面积有足够多，所以视他不算一个面积。

注意事项:

我的想法是，对于题目中给出的所有数据都扩大1000倍(长度单位扩大1000倍，面积单位扩大1000*1000倍)，也就是说将精度确定到小数点后三位这样计算。

题目说的是多个圆的阴影，而不是一个圆的，这是同样的，如果有多个圆覆盖了这个小格子的同一个点上，就判断这个小格子的被覆盖了一个点，算这个小格子是一个面积，如果多个圆覆盖了小格子的不同的点上，就算小格子被覆盖了多个点，不算一个面积。

这种情况，只判断他被覆盖了一个点，所以算一个面积

这种情况，就判断他被覆盖了两个点，所以不能算一个面积。

(当然，这只是我的规则，如果有更好的规则可以按照自己的规则来)

这种算法的确可以有效的得到一个近似的解，但是有一个很大的问题，就是精度低了得不到近似的答案，但是精度高了，所需要的时间就增加了，就不能在1s内得到求解，会存在超时的问题。希望各路神仙能够给出一点见解。

参考代码:

#include <iostream>
#include <cmath>
#define PI 3.1415926
using namespace std;
int main()
{
	int a,b,n,x[100],y[100],z[100],r[100];
	int sun_S=0,distance1=0; 
	double g,xi[100],yi[100],zi[100],ri[100];
	for(int i=0;i<100;i++)
	{
		x[i]=0;
		y[i]=0;
		z[i]=0;
		r[i]=0;
		xi[i]=0;
		yi[i]=0;
		zi[i]=0;
		ri[i]=0;
	}
	cin>>a>>b>>g>>n;
	for(int i=0;i<n;i++)
	{
		cin>>x[i]>>y[i]>>z[i]>>r[i];
		xi[i]=x[i]+z[i]*1/tan(g*PI/180.0);
		yi[i]=y[i];
		zi[i]=0;
		ri[i]=r[i];
		x[i]=xi[i]*1000;
		y[i]=yi[i]*1000;
		z[i]=zi[i]*1000;
		r[i]=ri[i]*1000; 
	}
	int farm_a=a*1000,farm_b=b*1000,flag=0;
	for(int i=0;i<farm_b;i++)
	{
		for(int j=0;j<farm_a;j++)
		{
			for(int z=0;z<n;z++)
			{
				distance1=sqrt( (j-x[z])*(j-x[z])+(i-y[z])*(i-y[z]) );
				if(distance1<r[z])
				{
					flag++;
					break;
				}
			}
			for(int z=0;z<n;z++)
			{
				distance1=sqrt( (j+1-x[z])*(j+1-x[z])+(i-y[z])*(i-y[z]) );
				if(distance1<r[z])
				{
					flag++;
					break;
				}
			}
			for(int z=0;z<n;z++)
			{
				distance1=sqrt( (j-x[z])*(j-x[z])+(i+1-y[z])*(i+1-y[z]) );
				if(distance1<r[z])
				{
					flag++;
					break;
				}
			}
			for(int z=0;z<n;z++)
			{
				distance1=sqrt( (j+1-x[z])*(j+1-x[z])+(i+1-y[z])*(i+1-y[z]) );
				if(distance1<r[z])
				{
					flag++;
					break;
				}
			}
			if(flag<2)
			{
				sun_S++;
				flag=0;
			}
			else flag=0;
		}
	}
	double answer=((double)(sun_S))/(1000*1000);
	printf("%.2lf",answer+0.01);
	return 0;
}