原题链接:不容易系列2
解题思路:
①:用全排列方法求出n=2,3...10的所有装法
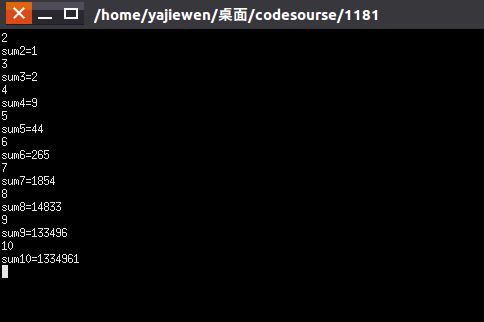
②:根据图得到以下规律:
(1)sum4=(sum2+sum3)*(4-1)
(2)sum5=(sum3+sum4)*(5-1)
(3)sum6=(sum4+sum5)*(6-1)
(4)sum7=(sum5+sum6)*(7-1)
....................
③:归纳总结得到:n个人信封装法数=(n-2个人的信封装法数+n-1个人的信封装法数 ) x (n-1)
注意事项:
结果不能用整型变量存储,n超过11长度不够;
参考代码:
#include<stdio.h>
int main()
{
int n,s=3;
double T,x=1,y=2;
while(scanf("%d",&n)!=EOF)
{
x=1,y=2,s=3; //x代表sum1,y代表sum2,s代表n-1
if(n==2)
printf("%.0lf\n",x);
else
if(n==3)
printf("%.0lf\n",y);
else
{
for(int i=0;i<n-3;i++) //根据规律循环次数为n-3,
{ //也可以用while循环
T=(x+y)*(s++); //等于下面注释部分
//T=(x+y)*s;
//s++;
x=y;
y=T;
}
printf("%.0lf\n",T);
}
}
return 0;
}全排列法:(不可提交)
#include<stdio.h>
#include<malloc.h>
void format(int *A,int N);
void pailie(int *A,int index,int length);
void swap(int *x,int *y);
void panduan(int *A,int N);
int sum=0;
int main()
{
int N;
int *A;
while( scanf("%d",&N)!=EOF)
{
sum=0;
A=(int *)malloc(N*sizeof(int));
format(A,N);
pailie(A,0,N);
printf("sum%d=%d\n",N,sum);
}
return 0;
}
/*===================================================*/
void format(int *A,int N)
{
for(int i=0;i<N;i++)
A[i]=i;
return;
}
/*===================================================*/
void pailie(int *A,int index,int length)
{
int i=0,j=0;
if(index==length)
{
panduan(A,length);
}
else
for(j = index;j < length; j++)
{
swap(&A[j],&A[index]);
pailie(A,index+1,length);
swap(&A[j],&A[index]);
}
return ;
}
/*===================================================*/
void swap(int *x,int *y)
{
int z=(*x);
(*x)=(*y);
(*y)=z;
return ;
}
/*===================================================*/
void panduan(int *A,int N)
{
int i;
for( i=0;i<N;i++)
{
if(A[i]==i)
break;
}
if(i==N)
sum++;
}别忘点赞哦-.-
0.0分
3 人评分
C语言网提供由在职研发工程师或ACM蓝桥杯竞赛优秀选手录制的视频教程,并配有习题和答疑,点击了解:
一点编程也不会写的:零基础C语言学练课程
解决困扰你多年的C语言疑难杂症特性的C语言进阶课程
从零到写出一个爬虫的Python编程课程
只会语法写不出代码?手把手带你写100个编程真题的编程百练课程
信息学奥赛或C++选手的 必学C++课程
蓝桥杯ACM、信息学奥赛的必学课程:算法竞赛课入门课程
手把手讲解近五年真题的蓝桥杯辅导课程

#include <stdio.h> int main(void) { int n = 0; while (1) { if (EOF == scanf("%d", &n))break; printf("%d\n", n-1); } return (0); }这样也行,这是个坑