python-数正方形

解题思路:

找规律。

参考了博客https://blog.csdn.net/qq_43319748/article/details/109655129

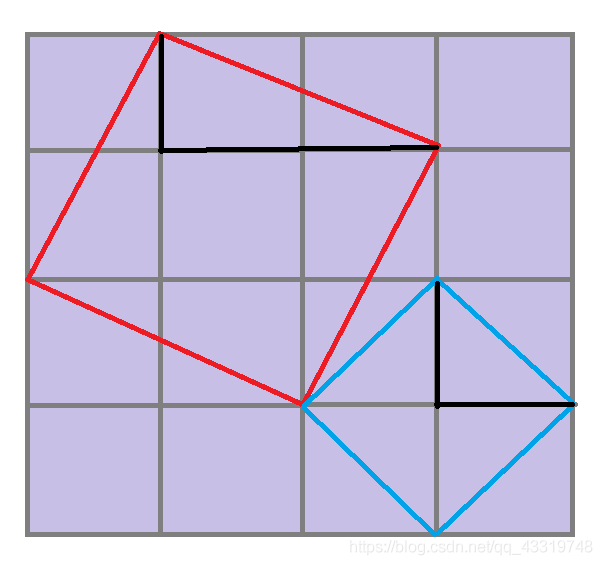
先解释一下（i*j）的斜正方形的概念。

例如上图红色正方形为（1*2）的斜正方形（这里的1和2分别是黑色边的长度）

       上如蓝色正方形为（1*1）的斜正方形（这里的1和1分别是黑色边的长度）

对于边长为1*1的正方形，有一个正放正方形，无斜放正放形

对于边长为2*2的正方形，有一个正放正方形，1个（1*1）的斜放正放形（总计两个正方形）

对于边长为3*3的正方形，有一个正放正方形，2个（1*2）的斜正方形（总计3个正方形）

对于边长为4*4的正方形，有一个正放正方形，2个（1*3）的斜正方形，1个（2*2）的斜正方形（总计4个正方形）

对于边长为5*5的正方形，有一个正放正方形，2个（1*4）的斜正方形，2个（2*3）的斜正方形（总计5个正方形）

对于边长为6*6的正方形，有一个正放正方形，2个（1*5）的斜正方形，2个（2*4）的斜正方形，一个（3*3）的斜正方形（总计6个正方形）

......

这里总结一下规律就是

对于边长为n*n的正方形，有一个正放正方形，2个（i*j）的斜正方形，（i+j=n，且1<=i<j）,当n为偶数时，再加1个（n/2*n/2）的斜正方形。

假设正方形有n*n的点组成，那么它的边长就是(n-1)*(n-1)

对于边长为1*1的正方形，一共有（n-1）*（n-1）个，那么正放的和斜放的加在一起就是（n-1）*（n-1）

对于边长为2*2的正方形，一共有（n-2）*（n-2）个，那么正放的和斜放的加在一起就是2*（n-2）*（n-2）

对于边长为3*3的正方形，一共有（n-3）*（n-3）个，那么正放的和斜放的加在一起就是3*（n-3）*（n-3）

对于边长为a*a的正方形，一共有（n-a）*（n-a）个，那么正放的和斜放的加在一起就是a*（n-a）*（n-a）

将所有可能边长的正方形结果累加就是最后结果

注意事项:

参考代码:

n = int(input().strip())  
sum = 0  
for i in range(1,n):  
    sum = (sum + i*(n-i)*(n-i)) % (10**9+7)  
  
print(sum)