蓝桥杯2017年第八届真题-对局匹配 （C语言代码）-------Five-菜鸟级

解题思路:
   动态规划  有点导弹拦截 的意思 

如果 用户积分之间相互有冲突  要想最多人 则需 每隔k积分的用户在线如下图
假设每个 积分段的用户 都一样的话 则要么取蓝色积分的用户 要么取红色用户都行

如果图片加载失败 则点击一下

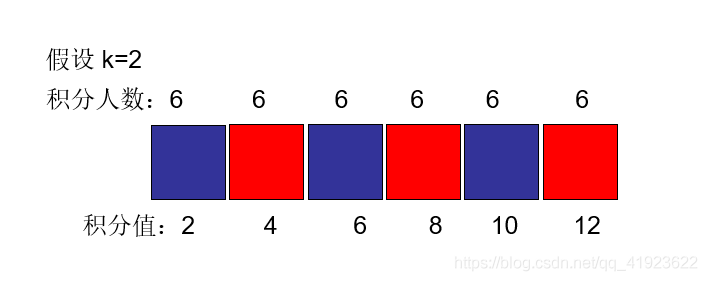
但是如果 积分人数如下图  肯定 每隔一个取得办法就不行了 正解 应该是看下面吧

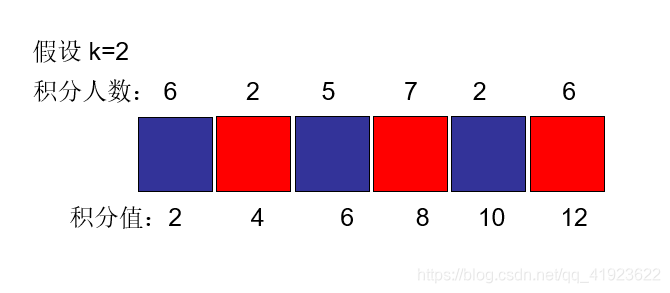
正解：取红色部分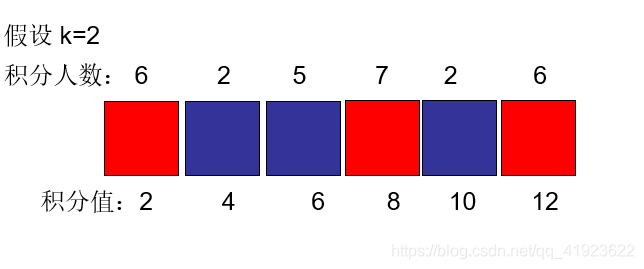

人眼看一眼就知道了 计算机 则需要动态规划的方式来到达目的 下面是该题的核心（理论就不讲了 讲讲具体实现 体会动态更新的过程）
从冲突用户第3个用户开始  那么他只能与他前前用户可以同时在线
所以 dp[6]=dp[2]+5=11   (dp[i]=k 代表 从第1个积分的用户到积分为i的用户 可同时在线的最大人数)
然后 更新一下 他 前面一个积分用户的dp[i-k]的值，为他后面一个积分的用户做准备  dp[i-k]=Max(dp[i-k],dp[i-2*k]);

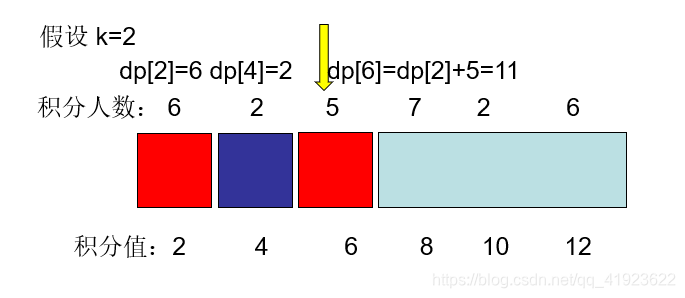
更新dp[i-k]    这个时候dp[i-k]=dp[4]=2就替换dp[i-2*k]=dp[2]=6 实质就是隔了2k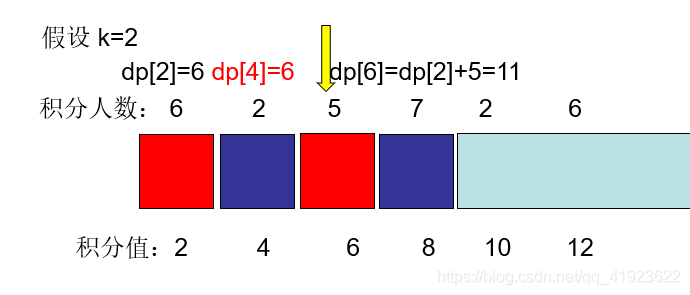

当处理第4个积分用户的 dp[8] 只需找他前前一个积分用户
然后更新他前一个 积分的用户 但是dp[i-k]>dp[i-2*k] 所以无需更新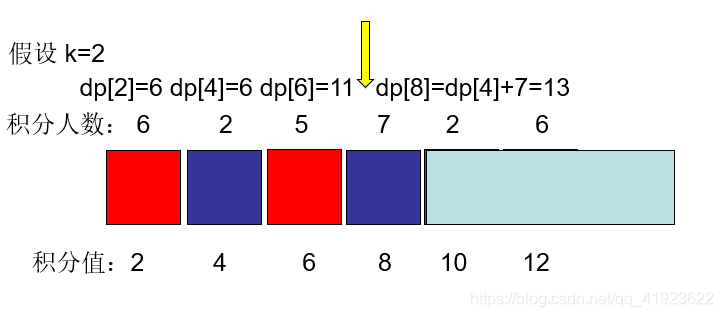

。。。。。
更新 到最后一个积分用户 就可以 得出当 积分为 2 4 6 8 10 12 这组相互冲突的用户之间 最大的可同时在线人数了

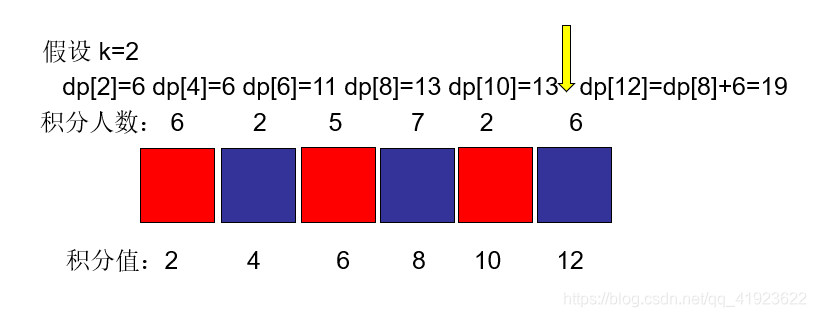
综上 ：
就可以得出
dp[i]=jf[i]+dp[i-2k];//从第1个积分用户到当前积分的最大人数
dp[i-k]=Max(dp[i-k],dp[i-2k]);//更新当前上一个积分用户
当然 也可以优化一下空间复杂度
用 dp替换dp[i]  qq_dp替换dp[i-2*k]   q_dp替换dp[i-k]
节省掉dp 开的空间
写为

   qq_dp=jf[ks]; q_dp=jf[ks+k]; for(i=ks+2*k;i<=js;i=i+k) {   
   dp=jf[i]+qq_dp;   //更新从第一到当前最大 积分只要至少隔一个k就行了 所以 本积分人数加上比他小两个k积分的用户人数
 q_dp=Max(q_dp,qq_dp);//更新前一个k积分用户  
 qq_dp=q_dp; q_dp=dp; }

AC代码1


#include <stdio.h>
#include <string.h>
long int jf[100012]={0};//jf[i]=k 代表积分为i的用户 有k个人
 long int n,k;
 long int Max(long int a,long int b ) { if(a>b)return a;else return b;}
 long int f(long int ks,long int js)
 {  long int i;
    long int dp[100012];
 	memset(dp,0,sizeof(dp));
   i=ks+2*k;           dp[ks]=jf[ks];dp[ks+k]=jf[ks+k];//初始化 前 2个 连续
//i从相互冲突的第3个人开始    第一用户    第二用户
	 for(i=ks+2*k;i<=js;i=i+k)
	 {   
	 	 dp[i]=jf[i]+dp[i-2*k];
	 	 //更新从第一到当前最大 积分只要至少隔一个k就行了 所以 本积分人数加上比他小两个k积分的用户人数
		 dp[i-k]=Max(dp[i-k],dp[i-2*k]);//更新前一个k积分用户  
	 }
	 return Max(dp[i-k],dp[i-2*k]);
 } 
int main()
{long int i,sum=0,s,max=0,t;
  scanf("%ld%ld",&n,&k);
  for(i=1;i<=n;i++)
  {  scanf("%ld",&s);
    jf[s]++;if(max<s)max=s;
  }
  if(k==0){//为0的时候特殊处理 每个积分 只允许1个人
  	for(i=0;i<=max;i++)if(jf[i]!=0)sum++;
  }else{
  for(i=0;i<=max;i++)
  {  if(jf[i]==0)continue;
	t=1;  while(jf[i+t*k]!=0)t++;//找出 有多少分数差k的用户（就是同时在线会冲突）
	 if(t!=1) sum+=f(i,i+(t-1)*k);//有冲突的人 的起始用户积分与结束用户积分
     else sum+=jf[i];//该积分就一个人 就不存在冲突 加上就好
	t=1;  while(jf[i+t*k]!=0) {jf[i+t*k]=0;t++;}//找过了就清零 
  }
}
printf("%ld\n",sum);
return 0;
}



AC代码2

#include <stdio.h>
#include <string.h>
int jf[100012]={0};//jf[i]=k 代表积分为i的用户 有k个人
int n,k;
int Max( int a, int b ) { if(a>b)return a;else return b;}
int f( int ks, int js)
{ int i;
int dp,q_dp,qq_dp;
qq_dp=jf[ks];q_dp=jf[ks+k];//初始化 前 2个 连续
//i从相互冲突的第3个人开始 第一用户 第二用户
for(i=ks+2*k;i<=js;i=i+k)
{
dp=jf[i]+qq_dp;
//更新从第一到当前最大 积分只要至少隔一个k就行了 所以 本积分人数加上比他小两个k积分的用户人数
q_dp=Max(q_dp,qq_dp);//更新前一个k积分用户
qq_dp=q_dp;q_dp=dp;
}
return Max(q_dp,qq_dp);
}
int main()
{int i,sum=0,s,max=0,t;
scanf("%d%d",&n,&k);
for(i=1;i<=n;i++)
{ scanf("%d",&s);
jf[s]++;if(max<s)max=s;
}
if(k==0){
for(i=0;i<=max;i++)if(jf[i]!=0)sum++;
}else{
for(i=0;i<=max;i++)
{ if(jf[i]==0)continue;
t=1; while(jf[i+t*k]!=0)t++;//找出 有多少分数差k的用户（就是同时在线会冲突）
if(t!=1) sum+=f(i,i+(t-1)*k);//有冲突的人 的起始用户积分与结束用户积分
else sum+=jf[i];//该积分就一个人 就不存在冲突 加上就好
t=1; while(jf[i+t*k]!=0) {jf[i+t*k]=0;t++;}//找过了就清零
}
}
printf("%d\n",sum);
return 0;
}