关于 完全背包 的解题思路（C++）

其实我是以前写01背包时无意中发现完全背包的 -__-#

（如果不会01背包，我建议先去学习一下）。

什么是完全背包？

在01背包中，每件物品可以取一次，而完全背包则是物品可以取无数次（只要背包容量充足）。

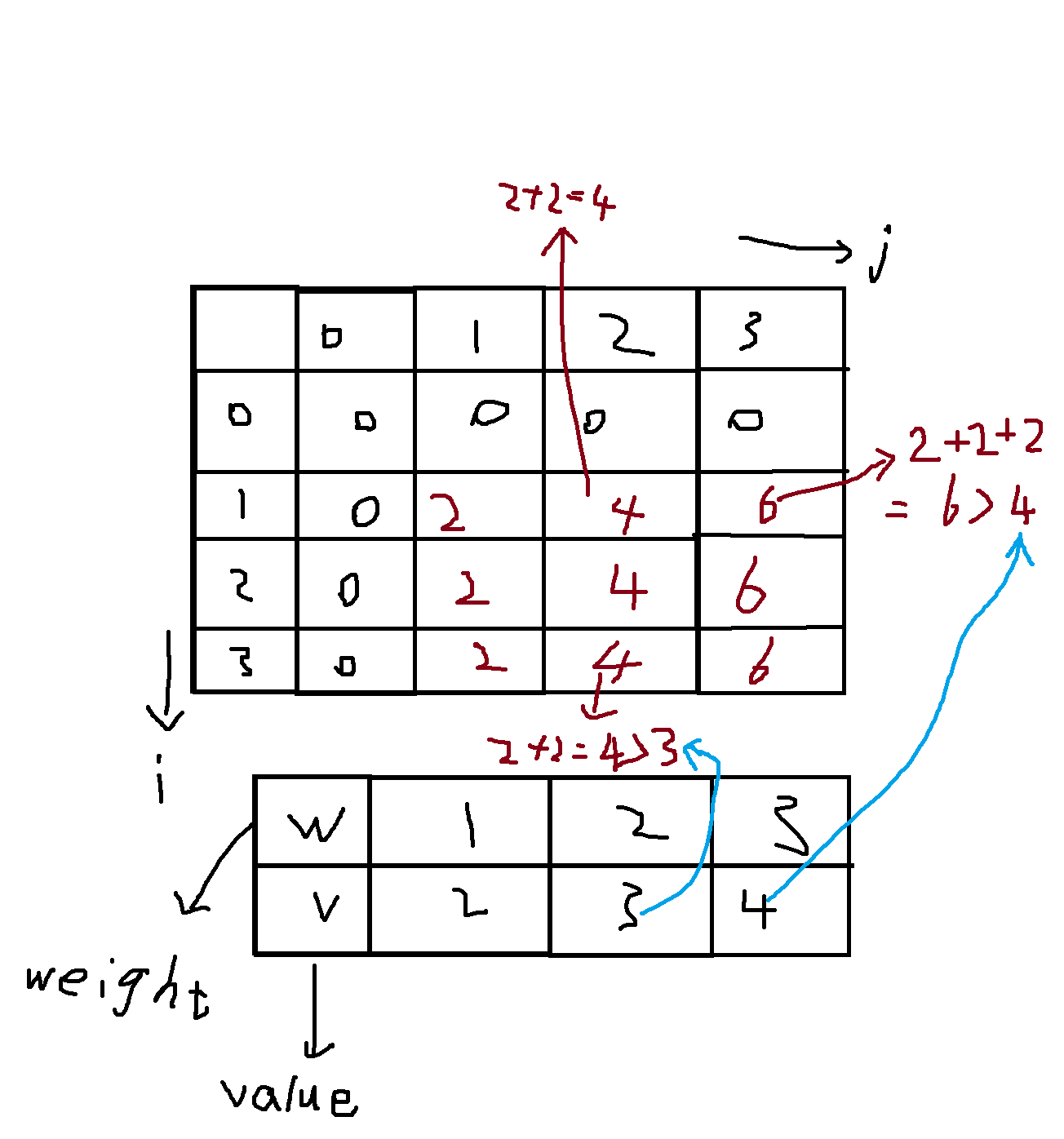
其中i代表物品数量，j代表物品重量。dp[i][j]表示当前背包容量为j时选择的最大价值。

第一次2+2是因为此时只有物品1可选；第二次2+2是因为背包容量为2时，选两次物品1价值最大。

其实完全背包的代码与01背包几乎一模一样，下面是代码：

#include<iostream>
#includeusing namespace std;

int main(){
    int w, v; // w是背包的最大承重，v是物品的数量
    cin >> w >> v; // 输入背包的最大承重和物品数量
    
    int dp[v + 1][w + 1]; // 创建一个二维数组来存储子问题的解
    int weight[w + 1], value[w + 1]; // 定义两个数组分别存储每个物品的重量和价值
    
    // 初始化dp数组为0
    for(int i = 0; i <= v; ++i){
        for(int j = 0; j  weight[i] >> value[i];
    
    // 动态规划计算最大价值
    for(int i = 1; i <= v; ++i){ // 遍历每一个物品
        for(int j = 1; j = weight[i]){ // 如果当前承重要大于等于当前物品的重量
                // 如果背包容量足够，则考虑带不带当前物品。
                    //注意，01背包与完全背包的区别就在这里：01背包是value[i] + dp[i - 1][j - weight[i]]，而完全背包是value[i] + dp[i][j - weight[i]]
                dp[i][j] = max(value[i] + dp[i][j - weight[i]], dp[i - 1][j]);//此时计算带上当前物品时的总价值，并与不带时的总价值进行比较，哪个大选哪个。
            } else {
                // 当前承重不够，则不带这个物品
                dp[i][j] = dp[i - 1][j];//继承上一层的状态（因为不带这个物品时，获取的最大价值与上一层相同，没变）
            }
        }
    }
    
    // 输出最终结果，即最大价值
    cout << "max=" << dp[v][w] << endl;
    return 0;
}

测试结果：