2604: 蓝桥杯2021年第十二届省赛真题-砝码称重（Java有set去重方法也有dp动态方法）要先看解释再看图

解题思路:

注意事项:    

将砝码独立来看，

在当前砝码称出重量x的情况下，对于砝码i都有三种操作：

x+砝码i的重量（放同侧）

x-砝码i的重量（放异侧）

x（不放）

显然前面两种操作才有可能产生不同的重量。

另外砝码i一定能称出其自身的重量

又考虑到set能够用于排除相等的元素

由于砝码称出的重量是正的，因此将操作获得的结果取绝对值再放入集合中

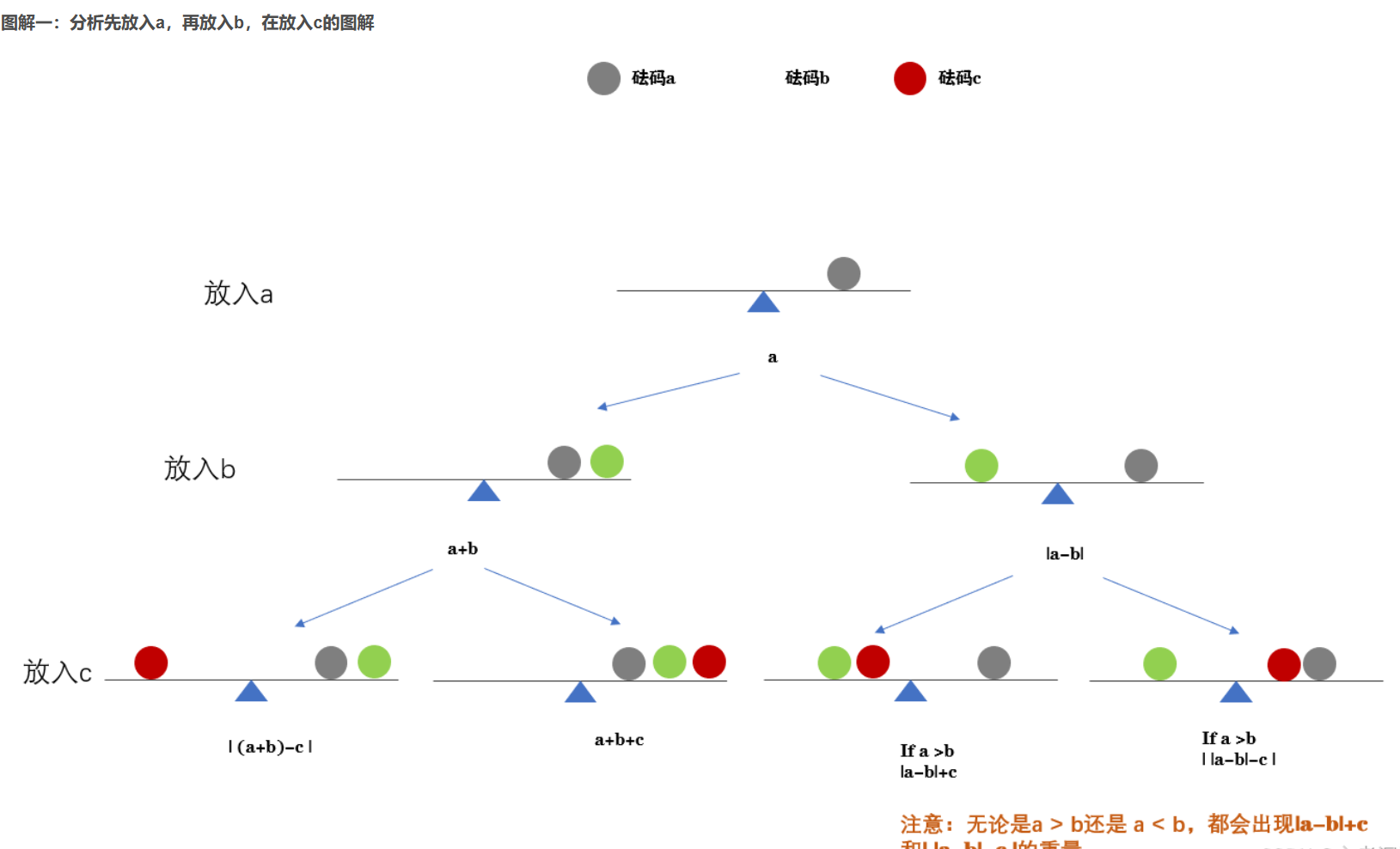
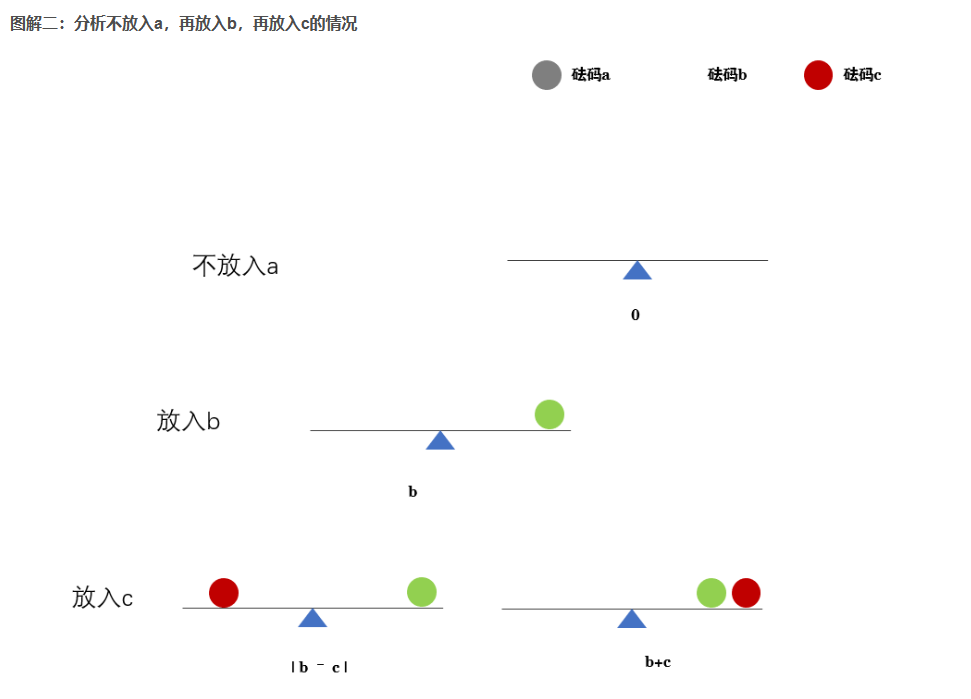
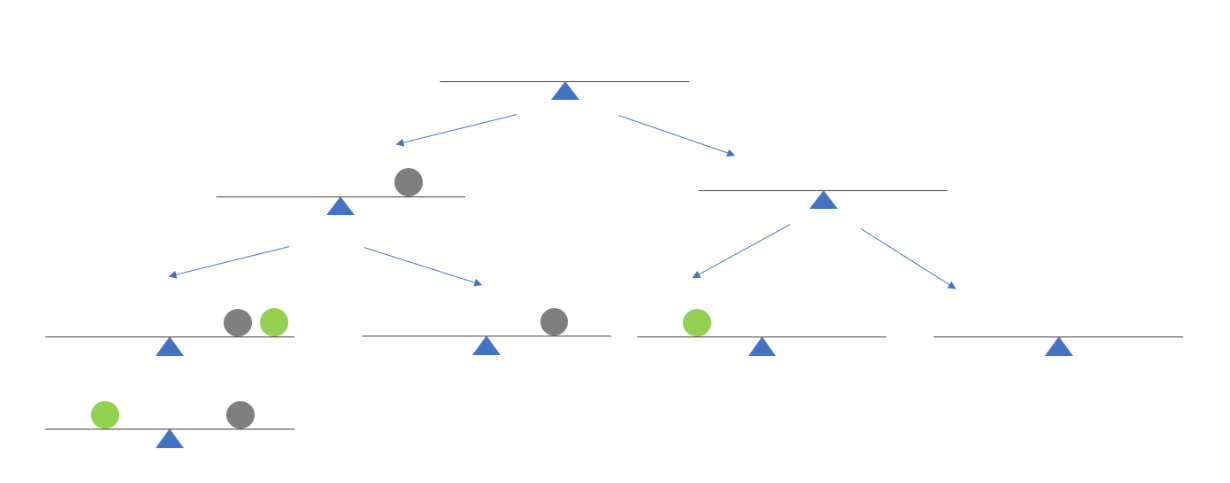
以上的图解只分析了两种情况 ，所有需要画出所有的情况，就会画出一颗树。

左子树代表选择放入新的砝码，右子树表示不放入新的砝码，也就是继承上次的重量。

注意：左子树可能会秤出两种重量

参考代码:

import java.util.*;
 
public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        Set<Integer> set = new HashSet<>();
        int n = scan.nextInt();
        int[] fama = new int[n];
        for (int i = 0; i < n; i++) {
            fama[i] = scan.nextInt();
        }
        //初始化set,表示一开始天平上没有砝码，重量为0
        set.add(0);
        for (int i = 0; i < n; i++) {
            //在没放入新的砝码前，将秤得的所有重量放入list集合中
            List<Integer> list = new ArrayList<>(set);
            for (int k : list) {
                //相加和相减取绝对值产生新的两个重量，并加重量放入set集合中
                //注意:如果新秤得的重量在原来的set集合存在，将不被放入set中
                set.add(k + fama[i]);
                set.add(Math.abs(k - fama[i]));
            }
        }
        //移除0元素
        set.remove((Object)0);
        //输出set集合大小，即秤得的重量数
        System.out.println(set.size());
    }
}

DP版本思路差不多

import java.util.Scanner;
public class Main{
	public static void main(String[] args){
		Scanner sc = new Scanner(System.in);
		int n = sc.nextInt();
		//存放砝码重量
		int a[] = new int[n];
		int sum = 0;
		for(int i = 0; i < n; i++){
			a[i] = sc.nextInt();
			sum += a[i];
		}
		
		int cnt = 0;
		boolean dp[][] = new boolean[n][sum+1];
	
		dp[0][a[0]] = true;
		
		for(int i = 1; i < n; i++){
			//将上一个状态复制过来
			for(int j = 1; j <= sum; j++)
				dp[i][j] = dp[i-1][j];
				
			dp[i][a[i]] = true;
			
			for(int j = 1; j <= sum; j++){
				if(dp[i-1][j]){
					dp[i][j+a[i]] = true;
					dp[i][Math.abs(j-a[i])] = true;
				}
			}
		}
		for(int i = 1; i <= sum; i++)
			if(dp[n-1][i])
				cnt++;
		System.out.println(cnt);
	}
}