【C语言】阶乘新问题：从暴力超时到精简代码 - DotcppXF

【解题思路】

        ① 末尾有多少个0的问题首先会想到10，一个数乘以10末尾就会多一个0，但直接统计10出现的次数显然不对；

        ② 事实上10是由5*2得来的，我们也能很快发现5乘以任何一个偶数就能得到整10的数；

        ③ 末尾0的数量实际上取决于5因子的数量，因为根据阶乘的定义，当5因子出现的时候偶数早就出现了，比如2和4；

        ④ 因此，统计出S(n)里面一共有多少个5因子成为本题解题的关键。

【1】暴力解法不可行

int count=0;
for(int i=1;i<=n;i++)
    for(int j=1;j<=i;j++)
        if(j%5==0)
            count++;

        上面的代码可能是最先能想到的最直接的统计方法了，但是实际上这样写存在三个方面的问题：

        ① 这样的统计方法本身就是错的，比如25这个数，只被统计了一次，但他有两个5因子；

        ② 效率太低，当数据很大的时候，暴力循环需要的时间太长，实际上本题的时间限制很严格，一不小心就会超时；

        ③ 本题没有说明数据范围，但测试数据实际上很大，建议用long或者long long来处理。

【2】寻找5因子数量的规律

        先来看从1到15的例子：

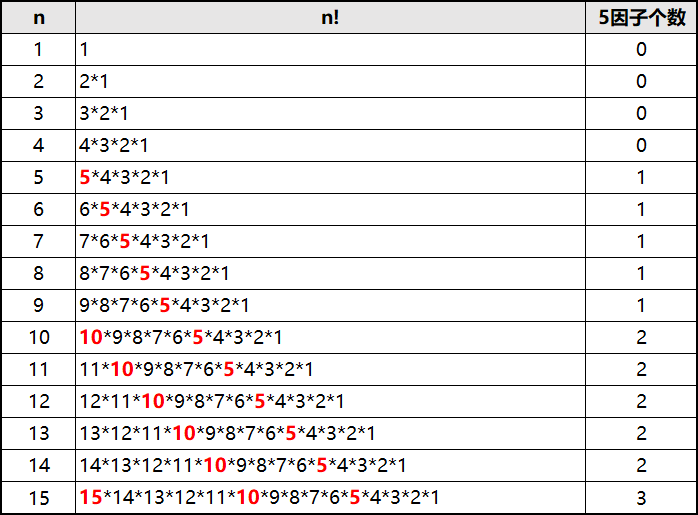
        通过上表可以发现 n! 中5因子的规律，每逢5的倍数，5因子增加1个；（暂未考虑25、125 ...... 的情况）

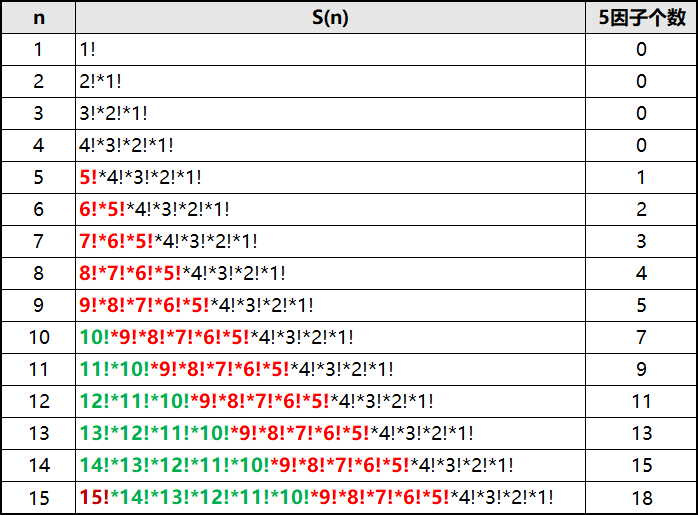
        通过上表可以发现 S(n) 中5因子的规律，每逢5的倍数，5因子的增长速度增加1个；（暂未考虑25、125 ...... 的情况）

long count=0;
for(long i=1;i<=n;i++)
    count+=i/5;

        ① 上面的代码是利用了 S(n) 与 S(n-1) 的关系，一项一项累加，只需要一层循环就可以了；

        ② 但是这样写还是会超时（不要问我怎么知道的），因此还需要找到效率更高的办法。

【3】换一种统计方式

        重新看回第一个表，实际上这整张表的因子就是 S(15) 的所有因子：

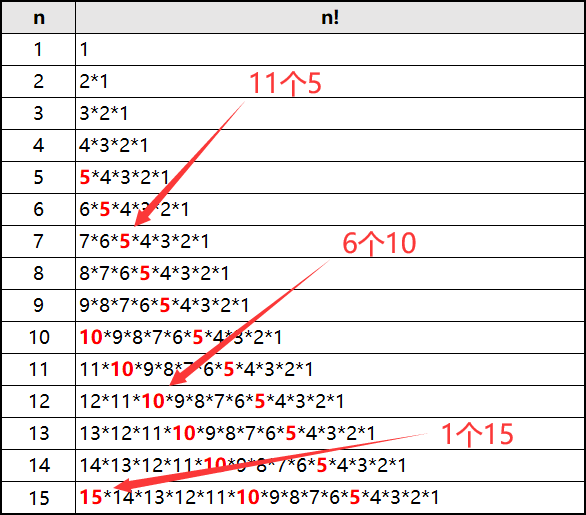
        那么表中的11、6、1这些数量是怎么算出来的呢？

        不难发现，11=15-5+1，其中15就是S(n)中的n，5表示第5行开始才有5出现，统计5出现的次数自然是15-5+1；

        同理6=15-10+1，表示10出现的次数，1=15-15+1，表示15出现的次数；

        由此可以推出，S(n) 中所有n-i+1的和就是所有5因子的个数，其中i是小于n的5的倍数，写成代码如下：

long count=0;
for(long i=5;i<=n;i+=5)
    count+=n-i+1;

【4】考虑5的指数的特殊情况

        ① 由于25、125、625等这些5的指数本身含有多个5因子，每次出现后就不能仅仅只统计1次。

        ② 再次统计它们的原理其实和统计5因子的原理一样，25因子在5因子的基础上再统计一遍，125因子在25因子的基础上再统计一遍，以此类推，最后累加的结果就是本题的最终答案：

long count=0;
for(long i=5;i<=n;i*=5)
    for(long j=i;j<=n;j+=i)
        count+=n-j+1;

【注意事项】

         ① 注意统计5因子时不要出错，特别是5的指数因子的时候；

         ② 数据范围建议用 long 或者 long long 来处理；

         ③ 代码效率要尽量提高，时间限制很严格。

【参考代码】

#include<stdio.h>
  
int main(void)
{
    long n,s=0;
    scanf("%ld",&n);
    for(long i=5;i<=n;i*=5)           // 循环5的指数：5、25、125、625 ......
        for(long j=i;j<=n;j+=i)       // 统计S(n)中5因子的个数，前面有解释，不再赘述
            s+=n-j+1;
    printf("%ld",s);
    return 0;
}