2034: 阴阳（种类并查集）

简单说一下思路：
这是带权并查集的一个分支种类并查集，阅读题目后可以分析出来，有两种关系，同类和吃，0为同类，1为吃。

查找：

举个例子

老鹰吃小鸡

      鹰->鸡1->鸡2

关系    1       0

那么如何路径压缩的时候如何操作？（鸡2为祖宗,re存的是当前数与父节点的关系）

我们只要(1+0)%2就可以得到鹰与鸡2的关系。

也就是说是（re[鹰]+re[鸡1]）%2；

合并

看图

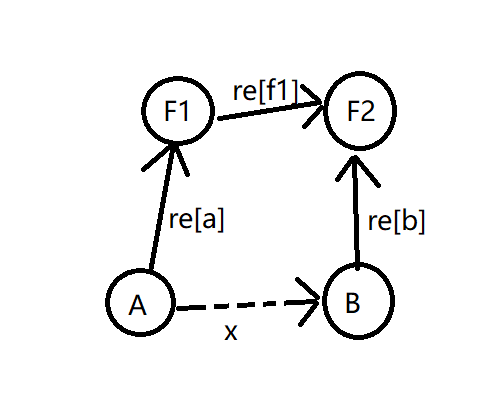
我们知道合并的时候是一个的祖宗链接到另一个祖宗后面

那么我们就要求F1与F2的关系看图我们可以得到

re[f1]=(re[b]+x-re[a]+2)%2;

+2是为了防止re[b]+x-re[a]<0;

最后判断两个数的关系

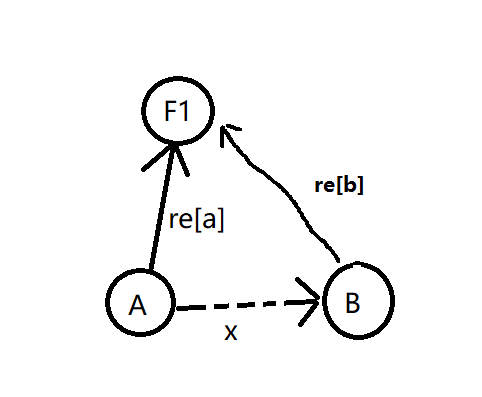
很明显是  x=(r[a]-re[b]+2)%2

说道这最好看代码吧

AC代码

#include<bits/stdc++.h>
using namespace std;
int f[30005],re[30005];
int n,m;
int find(int x)
{
	int p=f[x];
	if(x!=f[x])
	{
		f[x]=find(f[x]);
		re[x]=(re[x]+re[p])%2;
	}
	return f[x];
}
void merge(int x,int y,int z)
{
	int a=find(x);
	int b=find(y);
	if(x!=y)
	{
		f[b]=a;
		re[b]=(re[x]-re[y]+z+2)%2;//z为关系也就是图中的x
	}
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
	{
		f[i]=i;
		re[i]=0;
	}
	while(m--)
	{
		int x,y,z;
		scanf("%d%d%d",&x,&y,&z);
		merge(x,y,z);
	}
	int x,y;
	scanf("%d%d",&x,&y);
	if(find(x)!=find(y))//两个没有关系
	{
		printf("-1");
	}
	else
	{
		printf("%d",(re[x]-re[y]+2)%2);
	}
	return 0;
}