1665: 蓝桥杯算法训练VIP-连续正整数的和（前缀和+二分）

解题思路:
单纯暴力的话时间复杂度是O(n^3)，运算次数达到10^12次方，会超时，所以介绍一下前缀和算法，这是道很经典的前缀和的算法，大家可以通过这道题来理解前缀和的思想。

我们开辟一个数组，通过预处理将数组里面放进前n个数的和，例如p[4]=10就为1,2,3,4的和，通过p[n]-p[m-1]我们可以在O(1)的时间复杂度里得到[m,n]直接的和。

设 sumRange(i,j)为区间[i,j]直接的和，则数学表达就是：

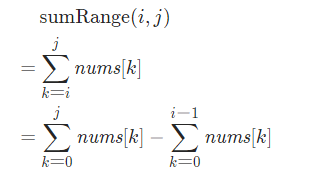
我们可以发现这里面有两个求和，所以我们可以提前预处理好1-n内的和，然后直接调用就可以了。

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h>

#define ll long long

ll p[10001];

int main (){
	ll i,j;
	ll n,m;
	scanf("%lld",&n);
	p[0]=0;
	for(i=1;i<=n;i++){
		p[i]=p[i-1]+i;
	}
	for(i=1;i<n;i++){
		for(j=i+1;j<n;j++){
			if(p[j]-p[i-1]==n){
				printf("%lld %lld\n",i,j);
			}
		}
	}
	
	
	return 0;
}

前缀和的时间复杂度是O(n^2)，题目的数据规模是一万，运算次数就是10^8，这是很危险的，如果达到十万的数据规模O(n^2)的时间复杂度是完全不行的了，所以这里提供一个O(nlog n)的算法：前缀和+二分

#include <stdio.h> // scanf printf
#include <stdlib.h>// qsort
#include <string.h>// strlen strcmp
#include <math.h>  // pow sqrt
#define ll long long
#define max(a,b) ((a)>(b)?(a):(b))

ll p[10001];

int main (){
	ll i,j;
	ll n,m;
	scanf("%lld",&n);
	p[0]=0;
	for(i=1;i<=n;i++){
		p[i]=p[i-1]+i;
	}
	for(i=1;i<n;i++){
		ll x=0,y=n;
		while(x<y){
			ll z=(x+y+1)>>1;
			if(p[z]-p[i-1]==n){
				printf("%lld %lld\n",i,z);
				break;
			}
			if(p[z]-p[i-1]<n)x=z;
			if(p[z]-p[i-1]>n)y=z-1;
		}
	}	
	
	return 0;
}

二分是查询中点来调整区间的算法，这种折半查找使得时间复杂度降到了log n级别。